Exam

Introduction

• data compression
  • process of converting an input data stream into output data stream that has a smaller size
  • compression algorithm = encoding (compression) + decoding (decompression)
  • compression
    • lossless – the restored and original data are identical
    • lossy – the restored data are a reasonable approximation of the original
  • methods
    • static / adapative
    • streaming / block
      • block – we compress the data by blocks
  • goals – to save storage, to reduce the transmission bandwidth
• measuring the performance
  • units
    • input data size … $u$ bytes (uncompressed)
    • compressed data size … $k$ bytes, $K$ bits
    • compression ratio … $k/u$ (written as percentage)
    • compression factor … $u:k$
    • compression gain … $(u-k)/u$ (written as percentage)
    • average codeword length … $K/u$ (may be bpc or bpp)
      • bpc … bits per char
      • bpp … bits per pixel
    • relative compression (percent log ratio) … $100\ln(k/k')$
      • $k'$ … size of data compressed by a standard algorithm
  • data corpora
    • Calgary Corpus – 14 files: text, graphics, binary files
    • Canterbury Corpus – 11 files + artificial corpus (4) + large corpus (3) + miscellaneous corpus (1)
    • Silesia Corpus
    • Prague Corpus
  • contests
    • Calgary Corpus Compression Challenge
    • Hutter Prize – Wikipedia compression
      • goal – encourage research in AI
• limits of lossless compression
  • encoding $f:$ {$n$-bit strings} → {strings of length $\lt n$}
    • $|\text{Dom}f|=2^n$
    • $|\text{Im}f|\leq 2^n-1$
    • such $f$ cannot be injective → does not have an inverse function
  • let $M\subseteq\text{Dom} f$ such that $\forall s\in M:|f(s)|\leq 0.9n$
    • $f$ injective on $M\implies|M|\leq2^{1+0.9n}-1$
    • $n=100$ … $|M|/2^n\lt 2^{-9}$
    • $n=1000$ … $|M|/2^n\lt 2^{-99}\approx 1.578\cdot 10^{-30}$
  • we can't compress all data efficiently (but that does not matter, we often focus on specific instances of data)

Lossless Compression

Statistical Methods

• basic concepts
  • source alphabet … $A$
  • coding alphabet … $A_C$
  • encoding … $f:A^*\to A^*_C$
  • $f$ injective → uniquely decodable encoding
• typical strategy
  • input string is factorized into concatenation of substrings
    • $s=s_1s_2\dots s_k$
  • substrings = phrases
  • $f(s)=C(s_1)C(s_2)\dots C(s_k)$
    • $C(s_i)$ … codeword
• codes
  • (source) code … $K:A\to A^*_c$
  • $K(s_i)$ … codeword for symbol $s_i\in A$
  • encoding $K^*$ generated by code $K$ is the mapping $K^*(s_1s_2\dots s_n)=K(s_1)K(s_2)\dots K(s_n)$ for every $s\in A^*$
  • $K$ is uniquely decodable $\equiv$ it generates a uniquely decodable encoding $K^*$
  • example
    • $\set{0,01,11}$ … is uniquely decodable
    • $\set{0,01,10}$ … is not, counterexample: $010$
    • $K_1$ … fixed length
    • $K_2$ … no codeword is a prefix of another one
• prefix codes
  • prefix code is a code such that no codeword is a prefix of another codeword
  • observation
    • every prefix code $K$ (over a binary alphabet) may be represented by a binary tree = prefix tree for $K$
    • prefix tree may be used for decoding
  • idea: some letters are more frequent, let's assign shorter codewords to them
    • historical example – Morse code
• Shannon-Fano coding
  • input – source alphabet $A$, frequency $f(s)$ for every symbol $s\in A$
  • output – prefix code for $A$
  • algorithm
    • sort the source alphabet by symbol frequencies
    • divide the table into parts with similar sums of frequencies
    • append 0/1 to prefix, repeat
  • divide and conquer algorithm
  • definition: the algorithm constructs an optimal prefix / uniquely decodable code $K\equiv$ $|K'^*(a_1a_2\dots a_n)|\geq |K^*(a_1a_2\dots a_n)|$ for every prefix (uniquely decodable) code $K'$ and for every string $a\in A^*$ with symbol frequencies $f$
  • Shannon-Fano is not optimal
    • Fano's student David Huffman described a construction of optimal prefix code

Huffman Code

• algorithm
  • constructs the tree from the bottom
  • starts with the symbols that have the lowest frequencies
  • sum of the frequencies is used as the frequency of the new node
• greedy algorithm
• optimality of Huffman code
  • notation
    • alphabet $A$ of symbols that occur in the input string
    • $\forall s\in A:f(s)$ … frequency of the symbol
    • let $T$ be a prefix tree for alphabet $A$ with frequencies $f$
      • leaves of $T$ … symbols of $A$
    • let $d_T(s)$ denote the depth of a leaf $s$ in the tree $T$
      • $d_T(s)=$ length of the path from root to $s$
      • $d_T(s)=$ length of the codeword for symbols $s$
    • cost $C(T)$ of tree $T$
      • $C(T)=\sum_{z\in A}f(z)d_T(z)$
      • $C(T)$ … length of the encoded message
  • lemma 0: if a prefix tree $T$ ($|V(T)|\geq 3$) contains a vertex with exactly one child, then $T$ is not optimal
  • proof: we could contract the edge between the vertex and its child
  • lemma 1
    • let $A$ ($|A|\geq 2$) be an alphabet with frequencies $f$
    • let $x,y\in A$ be symbols with the lowest frequencies
    • then there exists an optimal prefix tree for $A$ in which $x,y$ are siblings of maximum depth
  • proof
    • let $T$ be an optimal tree where $x,y$ are not siblings of maximum depth (instead, there are $a,b$ with maximum depth)
    • now by switching $a$ and $x$, we get $T'$
    • $C(T)-C(T')=d_T(x)f(x)+d_T(a)f(a)-d_{T'}(a)f(a)-d_{T'}(x)f(x)=$ $\dots\geq 0$
    • $T'$ is also optimal
    • we repeat the steps for $y$
    • we get $T''$
    • $T$ is optimal $\implies T''$ is optimal
  • lemma 2
    • let $A$ be an alphabet with $f$
    • let $x,y\in A$ be symbols with the lowest frequencies
    • let $T'$ be an optimal prefix tree for alphabet $A'=A\setminus\set{x,y}\cup\set{z}$ where $f(z)=f(x)+f(y)$
    • then tree $T$ obtained from $T'$ by adding children $x$ and $y$ to $z$ is an optimal prefix tree for $A$
  • proof
    • $T'$ optimal for $A'$
    • we get $T$ by adding $x,y$ below $z$ (therefore $z$ is no longer a symbol of the alphabet)
    • there exists $T''$ optimal for $A$ in which $x,y$ are siblings of maximum depth
      • using lemma 1
      • we label their parent $z$
    • we remove $x,y$ and get $T'''$ for $A'$
    • $C(T)=C(T')+f(x)+f(y)\leq C(T''')+f(x)+f(y)=C(T'')$
      • clearly $C(T')\leq C(T''')$ as $T'$ is optimal
    • $T''$ optimal $\implies T$ optimal
  • theorem: algorithm Huffman produces an optimal prefix code
    • proof by induction
  • theorem (Kraft-McMillan inequality)
    • codewords lengths $l_1,l_2,\dots,l_n$ of a uniquely decodable code satisfy $\sum_i 2^{-l_i}\leq 1$
    • conversely, if positive integers $l_1,l_2,\dots,l_n$ satisfy the inequality, then there is a prefix code with codeword lengths $l_1,l_2,\dots,l_n$
  • corollary
    • Huffman coding algorithm produces an optimal uniquely decodable code
    • if there was some better uniquely decodable code, there would be also a better prefix code (by Kraft-McMillan inequality) so Huffman coding would not be optimal
• idea: we could encode larger parts of the message, it might be better than Huffman coding
  • extended Huffman code … we use $n$-grams instead of individual symbols
• Huffman coding is not deterministic, there is not specified the order in which we take the symbols to form the tree – it may lead to optimal trees of different height
• can we modify Huffman algorithm to guarantee that the resulting code minimizes the maximum codeword length?
  • yes, when constructing the tree, we can sort the nodes not only by their frequencies but also by the depth of their subtree
• what is the maximum height of a Huffman tree for an input message of length $n$?
  • we find the minimal input size to get the Huffman tree of height $k$
    • how to make the tree as deep as possible?
    • the frequencies of the symbols will be Lucas numbers (with the zeroth number broken in two ones) or Fibonacci sequence – depending on the rules of the construction of the tree
  • Huffman tree of height $k\implies n\geq f_{k+1}$
    • where $f_0=1,\;f_1=1,\;f_{k+2}=f_{k+1}+f_k$
  • $n\lt f_{k+2}\implies$ max. codeword length $\leq k$
• there is an optimal prefix code which cannot be obtained using Huffman algorithm
• generalize the construction of binary Huffman code to the case of $m$-ary coding alphabet ($m\gt 2$)
  • the trivial approach does not produce an optimal solution
  • for the ternary coding alphabet, we can modify the first step – we will only take two leaves to form a subtree
• implementation notes
  • bitwise input and output (usually, we work with bytes)
  • overflow problem (for integers etc.)
  • code reconstruction necessary for decoding
• canonical Huffman code
  • if we know that the code contains 2 codewords of length 2 and 4 codewords of length 3, we can construct the code (we don't need to encode the tree)
  • 00, 01, 100, 101, 110, 111
• adaptive compression
  • static × adaptive methods
  • statistical data compression consists of two parts: modeling and coding
  • what if we cannot read the data twice?
    • we will use the adaptive model
• adaptive Huffman code
  • brute force strategy – we reconstruct the whole tree
    • after each frequency change
    • after reading $k$ symbols
    • after change of order of symbols sorted by frequencies
  • characterization of Huffman trees
    • Huffman tree – binary tree with nonnegative vertex weights
      • two vertices of a binary tree with the same parent are called siblings
      • binary tree with nonnegative vertex weights has a sibling property if
        • $\forall$ parent: weight(parent) = $\sum$ weight(child)
        • each vertex except root has a sibling
        • vertices can be listed in order of non-increasing weight with each vertex adjacent to its sibling (the weights are non-decreasing if we print them by levels, bottom to top, left to right)
    • theorem (Faller 1973): binary tree with non-negative vertex weights is a Huffman tree iff it has the sibling property
    • FGK algorithm (Faller, Gallagher, Knuth)
      • we maintain the sibling property
    • zero-frequency problem
      • how to encode a novel symbol
      • 1st solution: initialize Huffman tree with all symbols of the source alphabet, each with weight one
      • 2nd solution: initialize Huffman tree with a special symbol $esc$
        • encode the 1st occurence of symbol $s$ as a Huffman code of $esc$ followed by $s$
        • insert a new leaf representing $s$ into the Huffman tree
    • average codeword length … $l_{FGK}\leq l_H+O(1)$
  • implementation problems
    • overflow
      • we can multiply frequencies by $\frac12$
        • this may lead to tree reconstruction
      • statistical properties of the input may be changing over time – it might be useful to reduce the influence of older frequencies in time
        • by multiplying by $x\in(0,1)$
      • we'll use integral arithmetic → we need to scale the numbers

Arithmetic Coding

• each string $s\in A^*$ associate with a subinterval $I_s\subseteq[0,1]$ such that
  • $s\neq s'\implies I_s\cap I_{s'}=\emptyset$
  • length of $I_s=p(s)$
  • $C(s)=$ number from $I_s$ with the shortest code possible
• we'll first assume that $p(a_1a_2\dots a_m)=p(a_1)\cdot p(a_2)\cdot \ldots \cdot p(a_m)$
• encoding
  • we count the frequencies → probabilities
  • we sort the symbols in some order
  • we assign intervals to the symbols in the order
    • symbol with a higher frequency will be assigned a larger interval
  • to encode the message, we subdivide the intervals
    • for example, let's say that $I_B=(0.2,0.3)$ and $I_I=(0.5,0.6)$
    • then $I_{BI}=(0.25,0.26)$
  • the shorter the message, the longer the interval
  • we have to store the length of the input or encode a special symbol (end of file) to be able to distinguish between the encoded string and its prefixes
• decoding
  • we reconstruct the input string from the left
  • we inverse the mapping
• problem: using floating point arithmetic leads to rounding errors → we will use integers
  • underflow may happen that way if we use too short integers
• instead of individual frequencies of each symbol, we will use cumulative frequencies (it directly represents the intervals)
• if we have $b$ bits available to represent the current state, the (initial) interval can be $[0,2^{b}-1)$ or $[0,2^{b-1})$
• another problem
  • we use bit shifting and assume that the first bits of both bounds are the same
  • what if the first bits differ?
    • we don't output anything yet and increment a counter
  • it is similar to the situation (in real numbers) when we get to the range 0.53–0.67
    • we cannot write 5 or 6 and shift the number because we don't know whether the next range will be something like 0.53–0.56 or 0.63–0.67
    • we postpone the decision instead
• algorithm
  • start with the interval $[0,2^{b-1})$ represented as left bound $L$ and range $R$
  • encode each character of the block
  • if the range $R$ falls below $2^{b-2}$, we need to prevent underflow
    • if the current interval (range) starts in the first half of the interval $[0,2^{b-1})$ and ends in the second half, we don't output anything, only increment the counter and rescale the current interval
    • otherwise, we output one or more (most significant) bits of $L$ and rescale the current interval (also, we decrement the counter by printing the correct bits)
• time complexity
  • encoding $O(|A|+|\text{output}|+|\text{input}|)$
  • decoding $O(|A|+|\text{output}|+|\text{input}|\log|A|)$
  • it is also possible to make decoding faster by using more memory
    • we will represent the table of frequencies as an implicit tree
    • that way we can decode in time $O(|A|+|\text{output}|+|\text{input}|)$
• adaptive version
  • cumulative frequencies table as an implicit tree
  • Fenwick tree
    • Fenwick frequency = prefix sum (sum of all the weights of the lexicographically smaller vertices)

Theoretical Limits

• Hartley's formula
  • minimum and average number of yes/no questions to find the answer
  • if $x$ is a member of $n$ element set, then $x$ carries $\log_2 n$ bits of information
  • if we have a $k$-tuple of elements of $n$ elements set and $S_k$ is the least number of questions necessary to determine all $x_i$, then $S_k/k$ is the average number of questions necessary to determine one $x_i$
    • $|R|=n,\;x\in R^k$
    • $\log n^k\leq S_k\lt \log n^k+1$
    • $k\log n\leq S_k\lt k\log n+1$
    • $\log n\leq S_k/k\lt\log n+1/k$
• Shannon's formula
  • entropy … $H(X)=-\sum_{x\in R}p(x)\log p(x)$
  • theorem: $H(X)\geq 0$
  • lemma: Gibbs inequality
  • theorem: for a random variable $X$ with a finite range $R$, $|R|=n$, we have $H(X)\leq\log n$
    • and $H(X)=\log n\iff \forall x\in R:p(x)=\frac1n$
    • we plug it into the inequality … $q_i=\frac1n$
• Kraft-McMillan theorem
  • codeword lengths $l_1,l_2,\dots$ of a uniquely decodable code $C$ satisfy $\sum_i 2^{-l_i}\leq 1$
  • on the other hand, if natural numbers $l_1,l_2,\dots$ satisfy the inequality, then there is a prefix code with codewords of these lengths
• proof
  • let's start with $k$-th power of the sum of codeword lengths
  • $(\sum_{i=1}^n 2^{-l_i})^k=(\sum_{x\in R} 2^{-l(x)})^k$
  • we can rewrite that as the sum of products
    • and $l(x_{i_1})+l(x_{i_2})=l(x_{i_1}x_{i_2})$
  • therefore it is equal to $\sum_{x_{i_1}\dots x_{i_k}\in R^*}2^{-l(x_{i_1}\dots x_{i_k})}$
  • which equals $\sum_{i=1}^{k\cdot l_\text{max}}n(i)\cdot 2^{-i}\leq \sum_{i=1}^{k\cdot l_\text{max}}2^i\cdot 2^{-i}=k\cdot l_\text{max}$
  • now $\sum_{i=1}^n2^{-l_i}\leq\lim_{k\to\infty}(k\cdot l_\text{max})^{1/k}=1$
  • also, $R$ can be infinite
  • we can get the prefix code using arithmetic coding (probably?)
• theorem: let $C$ be a uniquely decodable code for a random variable $X$, then $H(X)\leq L(C)$
  • $L(C)$ … average codeword length
  • $L(C)=\sum_{x\in R} p(x)|C(x)|$
  • proof: by Gibbs inequality, we use $\frac{2^{-l_i}}{\sum_j 2^{-l_j}}$ as the second distribution
• entropy of a discrete random vector
  • $H(X)=nH(X_i)$
  • for independent components with the same probability distribution
• theorem: an arbitrary optimal prefix code $C$ for a random variable $X$ satisfies $H(X)\leq L(C)\lt H(X)+1$
  • proof of the upper bound: put $l_i=\lceil-\log p_i\rceil$, then Kraft-McMillan
  • this also holds for Huffman code (if we consider the entropy of one symbol)
• analysis of arithmetic coding
  • $H(X)\leq L(C)\lt H(X)+2$
    • $\overline{F(x)}=0.y_1y_2\dots$ is the midpoint of the interval for $x\in\mathbb R$ ($F$ is a CDF)
    • then $C(x)=y_1y_2\dots y_{l(x)}$ where $l(x)=\lceil\log\frac1{p(x)}\rceil+1$
    • in the proof, we show that $C$ is a prefix code
    • then, we use $L(C)=\sum p(x)\cdot l(x)$ which is upper bounded by $H(X)+2$
  • here, we don't consider one symbol but the whole message → therefore, the result is much better then the Huffman code
  • the main problem of the Huffman code is that it cannot deal very well with skewed probabilities of symbols as the lengths of the codewords must have integral length
• problems
  • we assume that the encoded random variables are independent
  • we are working with a probabilistic model of our data, which is simplified too much
• a better probabilistic model
  • we cannot use “unlimited” context – the probabilities would be too small
  • we will use the context of $k$ symbols
• according to an experimental estimate
  • the entropy of English is 1.3 bits per symbol

Context Methods

• model of order $i$ … makes use of context of length $i$
• methods
  • fixed length contexts
  • combined – contexts of various lengths
    • complete – all contexts of lengths $i,i-1,\dots,0$
    • partial
  • static, adaptive
• Prediction by Partial Matching (PPM)
  • Cleary, Witten, Moffat
  • uses arithmetic coding
  • we try to encode symbol $s$ in context of length $i$
  • if the context is too large (the frequency is not larger than zero), we output the ESC symbol and decrease the context length
  • assumption: every symbol has non-zero frequency for some (small) context
  • how to encode symbol $s$
    • we have read the context $c$ of length $i$ and the current symbol $s$
    • if $f(s\mid c)\gt 0$, encode $s$ using $f(*\mid c)$
      • each context $c$ has its own table of frequencies (for arithmetic encoding)
    • otherwise, output the code for ESC and try order $i-1$ context
  • exclusion principle
    • situation: symbol $x$ occurs in context $abc$ for the first time
    • we will encode it using second order model $f(x\mid bc)$
    • there is symbol $y$ such that $f(y\mid bc)\gt 0$ and also $f(y\mid abc)\gt 0$
    • by using ESC, we already signaled that we are not trying to encode any of the letters present in the third order model (such as $y$)
    • therefore, we can temporarily remove $y$ from the second order model so that the compression is more efficient
  • there are various approaches to assign $P(esc\mid c)$
    • for example, we can decrement frequencies of all symbols by one
  • data structure … trie (context tree)
    • where each node has an edge to its largest proper suffix, this simplifies adding of new leaves
    • it might not fit in the memory
      • to solve that, we can freeze the model (update frequencies in existing contexts, stop adding new contexts)
      • or we can rebuild the model using only the recent history (not the whole file)
    • we can rebuild the model either if the free memory size drops or if the relative compression ratio starts decreasing
  • advanced data structure: DAWG (Directed Acyclic Word Graph)
  • PPMII
    • “information inheritance”
    • uses heuristics
    • became part of RAR
  • PAQ
    • arithmetic coding over binary alphabet with sophisticated context modelling
    • using weighted average of probability estimates from various models
  • this algorithm has probably the best compression ratio
    • but it is very time and space consuming

Integer Coding

• unary code $\alpha$
  • $\alpha(1)=1$
  • $\alpha(i+1)=0\,\alpha(i)$
  • clearly, $|\alpha(i)|=i$
  • it is the optimal code for probability distribution $p(i)=2^{-i}$
• binary code $\beta$
  • is not a prefix code!
  • we can use fixed length
    • optimal code for $p(i)=\frac1{|A|}$
  • or we can gradually increase the codeword length as the dictionary size increases
• Elias codes
  • binary code always starts with 1
  • reduced binary code $\beta'$ … without the first 1
  • $\gamma'$ … first, we encode the length of the $\beta$ code using $\alpha$, then we encode the $\beta'$
  • $\gamma$ … we interleave the bits of $\alpha$ and $\beta$
  • $\delta$ … instead of $\alpha$, we use $\gamma$ to encode the length of $\beta$
  • we could construct other codes in a similar fashion but $\delta$ code suffices
    • for large numbers, it is shorter than $\gamma$
• Elias codes are universal
  • observation: each probability distribution $p_1\geq p_2\geq\dots\geq p_n$ satisfies $\forall i\in[n]:p_i\leq \frac1i$
  • corollary: $-\log p_i\geq -\log\frac1i=\log i$
  • $|\gamma(i)|=\log i+\Theta(\log i)$
  • $|\delta(i)|=\log i+o(\log i)$

Dictionary Methods

• idea
  • repeated phrases stored in a dictionary
  • phrase occurrence in the text → pointer
• problems
  • construction of the optimal dictionary is NP-hard → greedy algorithm
  • dictionary is needed for decoding → dynamic methods
• LZ77
  • Jacob Ziv, Abraham Lempel
  • sliding window
    • search buffer
    • look-ahead buffer
  • search for the longest string $S$ such that
    • $S$ starts in the search buffer
    • $S$ matches the prefix of the string in look-ahead buffer
  • $S$ is encoded as a triple $\braket{i,j,z}$ where
    • $i$ … distance of the beginning of $S$ from the look-ahead buffer
    • $j=|S|$
    • $z$ … the symbol following $S$ in the look-ahead buffer
  • example
    • ac|cabracad|abrarr|ar
    • ___\search/\lahead/__
    • $\to\braket{7,4,r}$
  • window slides $j+1$ symbols to the right
  • sliding window size $2^{12}-2^{16}\,B$, look ahead buffer size are usually tens or hundreds of bytes
  • slow compression, fast decompression
  • typical application – single compression, multiple decompressions
• LZSS
  • triple $(i,j,z)$ replaced with $(i,j)$ or literal $z$
    • bit indicator to distinguish one from another
  • if pair of pointers requires the same space as $p$ symbols, we use pairs to encode only phrases of length $\gt p$ (shorter phrases are simply copied to the output)
  • sliding window → cyclic buffer
  • possible implementation
    • codeword 16b, $|i|=11$, $|j|=5$
    • 8 bit indicators in 1 byte (one byte describes the types of 8 following items)
• other variants
  • LZB (LZSS with more efficient encoding of $(i,j)$ – using binary code with increasing length for $i$ and $\gamma$ code for $j$)
  • LZH (two-pass: LZSS, Huffman)
• Deflate algorithm
  • by Phil Katz, originally for PKZIP 2
  • zip, gzip, jar, cab, png
  • LZSS + static Huffman coding
  • search buffer size 32 kB
  • look-ahead buffer size 258 B
    • match length 3..258 → 256 options
    • for a smaller match, it uses literals
  • input divided into blocks
    • 3bit header
      • is it last block? (1b)
      • type of the block (2b)
    • 3 block types
      1. no compression
      2. static Huffman code compressed using trees defined in Deflate RFC
      3. dynamic Huffman code based on input data statistics
  • type 3 block
    • starts with two Huffman trees
    • the first tree for literals and match lengths
      • 0..255 for literals
      • 256 = end-of-block
      • 257..285 for match length (extra bits are used to distinguish between particular numbers)
    • the second tree for offset (again with extra bits)
  • hashing is used for string searching in search buffer
    • hash table stores string of length 3
    • strings in linked lists sorted by their age
    • a parameter to limit the maximum list length
  • greedy strategy extension
    • first, look for a primary match
    • slide window one symbol to the right, find a secondary match
      • if better, encode as literal + secondary match
• LZ77 disadvantages
  • limited outlook of the search window (longer window → better compression, more complex search)
  • limited length of the look-ahead buffer (match length limitation)
• LZ78
  • sliding window, explicit dictionary (but the directory is not transmitted)
  • efficient data structure for storing the dictionary … trie
  • compression
    • start with an empty dictionary
    • read the longest prefix of the input which matches some phrase $f$ in the dictionary (zero length is also possible – especially if the dictionary is empty)
    • output $\braket{i,k(s)}$
      • $i$ points to $f$ in the dictionary
      • $k(s)$ is a codeword for symbol $s$ which follows $f$ in the input
    • insert new phrase $fs$ into the dictionary
  • dictionary reconstruction is necessary when the dictionary space is exhausted
    • we can delete the whole dictionary
    • or delete only the phrases that occurred least frequently or have not occurred recently
    • we need to preserve the prefix property
      • if the dictionary contains $S$, it has to contain all prefixes of $S$
    • if compression ratio starts getting worse, we can delete the dictionary and start over
• LZW
  • we initialize the dictionary by the alphabet
  • we encode the longest prefix present in the dictionary
    • then, we append the next character and add it to the dictionary
  • when decoding, it may happen that the item is not in the dictionary yet
    • because the encoder is one step ahead
    • so we use the last decoded string and append its first character
  • we store only the pointers (and the alphabet?)
• LZC
  • compress 4.0 utility in Unix (LZC method is the implementation of LZW algorithm)
  • pointers into dictionary – binary code with increasing length (9–16 bits)
  • when maximum size was reached, it continues with static dictionary
  • when compression ratio started getting worse, it deletes the dictionary and starts over with the initial setting (we use a special symbol for that)
• LZMW
  • idea: new phrase = concatenation of two last ones (→ phrase length increases faster)
  • dictionary full → LRU strategy (delete the phrases that have not occurred recently)
  • dictionary lacks prefix property – this complicates searching, backtracking is used
• LZAP
  • idea: instead of $ST$ add all substrings $Sp$ where $p$ is a prefix of $T$
  • larger dictionary → longer codewords, wider choice for phrase selection
  • faster search → backtracking is not needed

Lossless Image Compression

• digital images – raster (bitmap), vector
• color spaces
  • RGB
  • CMYK
  • HSV
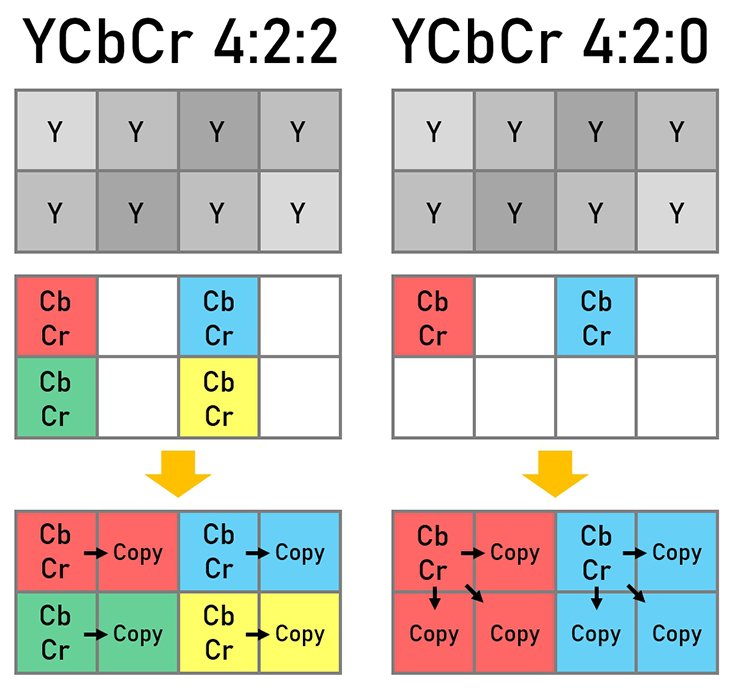
  • YUV – for backwards compatibility of the TV broadcast
• representation of bitmap images
  • monochrome
  • shades of gray
  • color
    • pixel = $(r, g, b)$
    • alpha channel
  • color palette
    • conversion table (pixel = pointer into the table)
    • types: grayscale (pallete with shades of gray), pseudocolor (color palette), direct color (three color palettes, one for each part of the color – R/G/B)
• GIF (Graphics Interchange Format)
  • usage
    • originally for image transmission over phone lines, suitable for WWW
    • sharp-edged line art with a limited number of colors → can be used for logos
    • small animations
    • not used for digital photography
  • color palette, max. 256 colors
    • supports “transparent” color
  • multiple images can be stored in one file
  • supports interlacing
    • rough image after 25–50 % data
    • we can stop the transmission if it's not the image we wanted
    • 4-pass interlacing by lines
  • LZW-based compression (actually, it uses LZC)
  • pointers … binary code with increasing length
  • blocks … up to 255 B
  • we can increase the number of possible colors by stacking multiple images on top of another (and using transparent pixels)
• PNG (Portable Network Graphics)
  • motivation: replace GIF with a format based on a non-patented method (LZW was patented by Sperry Corporation / Unisys)
  • color space – gray scale, true color, palette
  • alpha channel – transparency $\in[0,1]$
  • supports only RGB, no other systems (it was designed for transferring images over the network)
  • compression has two phases
    • preprocessing – predict the value of the pixel, encode the difference between the real and predicted value (prediction based on neighboring pixels)
      • prediction types: none, sub (left pixel), up, average (average of sub and up), Paeth (more complicated formula)
      • each line may be processed with a different method
    • dictionary compression
      • deflate (LZ77)
  • supports interlacing
    • 7-pass interlacing by blocks of pixels
    • 
  • single image only, no animation

Burrows-Wheeler Transform

• BSTW
  • Bentley, Sleator, Tarjan, Wei
  • move to front heuristic to restructure the dictionary
  • we start with an empty dictionary $D$
  • for input word $s$
    • if $s$ s in dictionary $D$ on position $i$, we output $\gamma(i)$ and move $i$-th word in $D$ to the front of $D$
    • otherwise, we output $\gamma(|D|+1)$ and $s$ itself, we insert $s$ to the front of $D$
• Burrows–Wheeler transform
  • we are looking for a permutation of string $x$ such that the similar symbols are close to each other
  • matrix of cyclic shifts of $x$
    • sort rows lexicographically
    • the desired permutation is the last column
    • also, we need to store a number of the row where the original string lies in the matrix to be able to restore the original
    • if we used the first column, it would not be decodable
  • encoding
    • MTF (move to front) heuristic
      • for each symbol, its code would be the number of preceding symbols in the dictionary
      • then, move the symbol to the front of the dictionary
      • therefore, the number we use to encode the symbol matches the time that elapsed from the last encoding of that symbol (if it was encoded previously)
    • RLE … run length encoding
      • instead of $n$ zeros, we can just encode the zero and length of the block
    • Huffman/arithmetic coding
  • decoding
    • how to obtain the original string from the last column and the number?
    • we sort the last column to get the first one
    • we can determine the penultimate symbols from the pairs of first and last – thanks to the cyclic shift
      • what if there are multiple lines that end with the same symbol? we know that the lines were sorted lexicographically
  • matrix $n×n$ is not neccessary
    • we can use suffix array
    • this would be equivalent to the matrix of rotations of x$, where xis the original string and $ is a sentinel character
  • why does BW transform work?
    • two same letters often share very similar right context
    • therefore they will be close in the rightmost column
    • (we are actually sorting the letters by their right context)
• bzip2
  • Julian Seward
  • open source
  • has more efficient compression than gzip/zip
    • but bzip2 is slower
    • it does not support archiving
      • it can only compress single
      • just like gzip
      • can be used to compress tar archives
  • compression
    • split the input into blocks of 100–900 kB (determinted by an input parameter)
    • Burrows–Wheeler transform
    • MTF, RLE
    • arithmetic coding (patented) was replaced with Huffman coding

Lossy Compression

• no standard corpora exist
• how to measure the loss of information
  • mean squared error (MSE)
  • signal to noise ratio (SNR)
  • peak signal to noise ratio

Digitizing Sound

• sound is a physical disturbance in a medium, it propagates as a pressure wave
• Fourier theorem
• sampling
  • Nyquist-Shannon sampling theorem
  • the sampling frequency should be at least twice the highest frequency we want to record
  • if the condition fails, it leads to aliasing (zkreslení)
    • there appear false frequency components that were not present in the original analog signal
    • for sampling frequency $F_s$ and original $f\gt\frac12F_s$, the new false frequency will be $f'=F_s-f$
  • example: the carriage (or stagecoach) wheels in the movie are spinning backwards
• quantization
  • we have $B$ bits available
  • we split the whole interval into $2^B$ subintervals
• we want the largest signal to noise ratio that is possible
• audio processing
  • input
    • amplifier
    • band-pass filter
    • sampler … sampling
    • A/D converter … quantization
    • RAM
  • output
    • RAM
    • D/A converter
    • band-pass filter
    • amplifier

Quantization

• main idea
  • large set → smaller set
  • quantizer can be scalar or vector
  • quantization consists of two mapping – encoding and decoding
• central limit theorem
  • if we collect $n$ samples of random variable $X$, the distribution of the sample mean approaches $N(\mathbb EX,\text{var}(X)/2)$ for a sufficiently large $n$
• problem formulation
  • source … random variable $X$ with density $f(x)$ (common assumption – $f$ is symmetric about 0)
  • determine: number of intervals (levels), interval endpoints (decision boundaries), representative $y_i$ for each interval (reconstruction levels)
  • goal: to minimize the quantization error (distortion) $\sigma^2$ … MSE
    • $\sigma^2=\mathbb E[(x-Q(x))^2]$
  • the number of intervals (levels) may be fixed if we want fixed length codewords
• uniform quantizer
  • uniform probability distribution
  • all intervals of equal length
  • two types
    • midrise quantizer – even number of levels, $Q(0+\varepsilon)\neq 0$ (zero is a decision boundary)
    • midtread quantizer – odd number of levels, $Q(0+\varepsilon)=0$ (zero is in the middle of the central interval)
  • we assume that the range of $X$ is bounded
• forward adaptive quantizer (offline)
  • split the input into blocks
  • analyze each separately, set parameters accordingly
  • parameters are transmitted as side information
• backward adaptive quantizer (online)
  • no side info necessary
  • Jayant quantizer
    • multipliers
    • intervals can shrink and expand depending on the input
    • for each input value, we get the corresponding code $c$ and we multiply $\Delta$ by the multiplier $M_c$
    • the intervals automatically adapt to the input data
    • 3bit Jayant quantizer
      • table of intervals

• nonuniform quantization
  • we set $y_j$ to the average value in the interval
    • $y_j=\frac{\int_{b_{j-1}}^{b_j}xf(x)dx}{\int_{b_{j-1}}^{b_j}f(x)dx}$
  • we set the interval bounds as the averages of neighboring values
    • $b_j=\frac{y_{j+1}+y_j}{2}$
  • Lloyd-Max algorithm
    • $M$-level symmetric quantizer
    • we set $b_0=0$
    • we somehow approximate $y_1$
    • then we compute $b_1$ from the equation for $y_j$ stated above
    • $y_2=2b_1-y_1$ (similarly $b_2,y_3,\dots$)
    • note: the $b$ bounds and $y$ values are symmetrical, $y_{-1}=y_1$ etc.
    • computation depends on the initial estimate $y_1$
      • we want to correct our wrong estimate
      • we know that $b_{M/2}$ = max input value
      • we can compare the resulting $y_{M/2}$ with the value $y^*_{M/2}$ computed using the quotient of integrals
      • if they differ too much, we correct the initial estimate of $y_1$ and repeat the whole procedure
• companding
  • compressing + expanding
  • first we stretch the high probability regions close to the origin & compress the regions with low probability
  • then apply uniform quantization
  • expand afterwards (transform quantized values to the original scale)
  • $\mu$-law
    • telephony, USA, Japan
    • $\mu=225$
    • there is $c(x)$ which compresses the values and $c^{-1}(x)$ which expands them (there is the constant $\mu$ in the formulas)
  • A-law
    • telephony, Europe
    • $A=87.6$
    • there are different $c(x)$ and $c^{-1}(x)$ then in $\mu$-law
  • G.711
    • ITU-T standard for audio companding
    • sampling frequency 8 kHz
    • sample length is 14b ($\mu$-law) or 13b (A-law)
    • $\mu$-law uses midtread quantizer
    • A-law uses midrise quantizer
    • comparison
      • $\mu$ … higher dynamic range, noise reduction in blocks of silence (thanks to midtread)
      • A … lower relative distortion of small values
    • application: VoIP

Vector Quantization

• we split the file (or group the individual samples) into vectors
  • $L$ consecutive samples of speech
  • block of $L$ pixels of an image (a rectangle/square)
  • → vector of dimension $L$
• idea: codebook
  • code-vectors selected to be represented, each one has a binary index
  • encoder finds the closest vector in the codebook (using Euclidean distance or MSE)
  • decoder retrieves the code-vector given its binary index
  • codebook size $K$ → $K$-level vector quantizer
  • we can design the codebook using k-means algorithm (or we can use LBG as described below)
• LBG algorithm
  • Linde, Buzo, Gray
  • we have codebook $C$, training set $T$, threshold $\varepsilon$
  • we can compute quantization regions – assign each input vector to its code-vector
  • we can compute the average distortion (MSE) in each step of the algorithm
    • if it is less than the threshold, we can return the codebook
    • otherwise, we need to update it (we set the code-vector to the average of all the input vector in its group – like in k-means)
  • initialization
    • LBG splitting technique
      • start with a single code-vector – the average of all vectors in the training set
      • in each step we generate a perturbation vector, add it to each code-vector and introduce those new vectors to the codebook → the codebook size doubles
        • then, we run LBG with the codebook (repeatedly update the code-vectors until the distortion drops below certain level)
      • we repeat this until the desired number of levels is reached
    • random init (Hilbert)
      • initialize $C$ randomly several times
      • select the alternative with lowest distortion
    • pairwise nearest neighbor (Equitz)
      • start with $C=T$
      • in each step, replace two code-vectors by their mean
      • goal: smallest increase in distortion
  • it is possible that during the algorithm, we are left with a code-vector that does not have any corresponding training set vectors (“empty cell problem”) → we will replace it with a new code-vector chosen randomly from the cluster with the highest population of training vectors or the highest associated distortion
• tree-structured vector quantization (TSVQ)
  • when quantizing a vector, we don't want to compare it to each vector in the codebook
  • we will divide the codebook into two groups such that there exists two test vectors that all vectors from the first group are closer to the first vector (and vice versa)
  • we repeat the process → binary tree
  • pros: we need a lower number of comparisons, we can build a binary string (code) as we progress down the tree
  • cons: increased storage requirement (we need to store the test vectors, the codebook does not suffice), possible increase in distortion
  • we may use LBG splitting technique to get test vectors
    • we need to modify the technique, we will always run LBG only with two code-vectors and the corresponding subset of the test set
  • pruned TSVQ
    • we can remove some subtrees to decrease the average rate (codeword length) – but this will increase average distortion
    • also, we can split some nodes
    • this way, we get binary codewords of variable length, the codewords correspond to paths in the decision tree → prefix code
• lattice vector quantizers
  • idea: regular arrangement of code-vectors in space
    • quantization regions should tile the output space of the source
  • D lattices
    • $D_2$ lattice (in two-dimensional space)
      • $a\cdot v_1+b\cdot v_2=a(0,2)+b(1,1)=(b,2a+b)$
      • squares
    • the sum of the coordinates is always even
  • A lattices
    • $A_2$ lattice is hexagonal
  • G.719
    • ITU-T standard for wideband audio coding
    • modified dicrete cosine transform (DCT)
    • vector quantizer based on $D_8$ lattice
• classified vector quantization
  • idea: divide source vectors into classes with different properties, perform quantization separately
  • example: edge/nonedge regions (in an image)
    • large variance of pixels $\implies$ presence of an edge (will use edge codebook for this vector)
    • output has to contain the codebook label and the vector label
• applications
  • audio: G.719, CELP, Ogg Vorbis, TwinVQ
  • video: QuickTime, VQA

Differential Encoding

• idea: consecutive samples are quite similar (that holds especially for speech and images)
• if we quantize the differences directly, the error will accumulate
• instead of that, we will quantize the difference between the previous predicted value and the current value
  • or we can use a more general function of multiple previous predicted values instead of just the last value
  • this function can be called $p_n$
• DPCM (differential pulse-code modulation)
  • C. Chapin Cutler, Bell Labs
  • goal: minimize MSE (error between the real value and $p_n$)
  • linear predictor $p_n=\sum_{i=1}^N a_i\hat x_{n-i}$
    • where $\hat x_k$ is $k$-th predicted value
  • problem: find $a_j$ which minimize MSE
    • set the derivative w.r.t. $a_j$ equal to zero
    • $\forall j:-2\mathbb E[(x_n-\sum a_ix_{n-i})x_{n-j}]=0$
    • $\mathbb E[(x_n-\sum a_ix_{n-i})x_{n-j}]=0$
    • $\mathbb E[x_nx_{n-j}]=\sum a_i\mathbb E[x_{n-i}x_{n-j}]$
    • we can rewrite this using autocorrelation $R_{XX}(k)=\mathbb E[x_nx_{n+k}]$
    • we get Wiener-Hopf equations (matrix multiplication)
    • we will estimate $R_{XX}(k)$ – nothing complicated, it's just an average of products
      • we assume that the process is stationary
• ADPCM
  • adaptive DPCM
  • forward adaptive prediction (DPCM-APF)
    • estimate autocorrelation for blocks
    • we need to transfer coefficients and buffer the input (group it into blocks)
  • backward adaptive prediction (DPCM-APB)
    • no need to transfer additional info
    • we will use stochastic gradient descent during coding (LMS = least mean squares algorithm)
    • $A^{(n+1)}=A^{(n)}+\alpha \hat d_n\hat X_{n-1}$
• G.726
  • ITU-T standard for speech compression based on ADPCM
  • predictor uses two latest predictions and six latest differences (between predicted values)
  • simplified LMS algorithm
  • backward adaptive quantizer (modified Jayant)
• delta modulation
  • speech coding
  • very simple form of DPCM
  • 2-level quantizer (we can only encode $+\Delta$ or $-\Delta$)
  • we need really high sampling frequency
  • problems
    • constant signal (we encode it as a sequence of ↑↓↑↓↑↓↑↓)
      • “granular regions”
    • a slope steeper than delta
      • “slope overload region”
  • solution: adapt $\Delta$ to the characteristics of the input
• constant factor adaptive delta modulation (CFDM)
  • objective: increase delta in overload regions, decrease it in granular regions
  • how to identify the regions?
    • use a history of one sample (or more)
  • application: space shuttle ↔ ground terminal (CDFM with 7-sample memory)

Transform Coding

• scheme: group individual samples into blocks, transform each block, quantization, coding
• for images, we have to make a two-dimensional transform
  • it is better to transform each dimension separately = separable transform
• separable transform using matrix $A$
  • transformed data $\Theta=AXA^T$
  • original data $X=A^{-1}\Theta(A^{-1})^T$
• orthogonal transform … we use orthogonal transform matrix
  • transformed data $\Theta=AXA^T$
  • original data $X=A^T\Theta A$
  • moreover $\sum_i \theta_i^2=\sum_i x_i^2$
  • gain $G_T$ (of a transform $T$) = arithmetic over geometric mean of $\sigma_*^2$
    • $\sigma_i^2$ … variance of coefficient $\theta_i$
• Karhunen-Loéve transform
  • minimizes the geometric mean of the variance of the transform coefficients
  • transform matrix consists of eigenvectors of the autocorrelation matrix $R$
  • problem: non-stationary input → matrix $R$ changes with time → KLT needs to be recomputed
• discrete cosine transform
  • DCT is the “cosine component” of DFT
  • redistributes information so that we can quantize it more easily
  • why is DCT better than DFT?
    • FT requires a periodic signal
    • periodic extension of non-periodic signal would introduce sharp discontinuities and non-zero high-frequency coefficients
  • DCT may be obtained from DFT (start with the original non-periodic signal consisting of $N$ points, mirror it to get $2N$ points, apply DFT, take the first $N$ points)
  • DCT transform matrix – 1st row is constant vector, following rows consist of vectors with increasing variation
    • these are the portions of the original “signal” (data matrix $X$) that the coefficients in the $\Theta$ matrix correspond to
    • 
      • these can be called “basis matrices”
    • basis matrix corresponding to $\theta_{11}$ is a constant matrix $\implies$ $\theta_{11}$ is some multiple of the average value in the data matrix
      • $\theta_{11}$ … DC coefficient
      • other $\theta_{ij}$ … AC coefficients
  • gain $G_{DCT}$ is close to the optimum value for Markov sources with high correlation coefficient $\rho=\frac{\mathbb E[x_nx_{n+1}]}{\mathbb E[x_n^2]}$
• discrete sine transform
  • gain $G_{DST}$ is close to the optimum value for Markov sources with low correlation coefficient $\rho=\frac{\mathbb E[x_nx_{n+1}]}{\mathbb E[x_n^2]}$
• Hadamard matrix
  • square matrix of order $n$ such that $HH^T=nI$
  • $H_1=(1)$
  • $H_{2n}=\begin{pmatrix} H_n & H_n \\ H_n & -H_n \end{pmatrix}$
• discrete Walsh-Hadamard transform
  • DWHT transform matrix is a rearrangement of $H_n$
    • multiply $H_n$ by normalizing factor $\frac1{\sqrt n}$
    • reorder the rows by increasing number of sign changes
  • pro: speed
  • con: $G_{DWHT}\ll G_{DCT}$
• quantization of transform coefficients
  • zonal sampling
    • coefficients with higher expected variance are assigned more bits for sampling
    • pro: simplicity
    • con: bit allocations based on average rules → local variations (e.g. sharp edges on plain background) might not be reconstructed properly
• quantization and coding
  • threshold coding
    • based on the threshold, we decide which coefficients to keep (or discard)
    • we have to store the numbers of discarded coefficients
    • threshold is not decided a priori
  • Chen & Pratt suggest zigzag scan
    • tail of the scan should consist of zeros (generally, the higher-order coefficients have smaller amplitude) → for fixed length of the block, we don't need to specify the number of zeros, just send end-of-block (EOB) signal
    • note: DC coefficients correspond to contours, higher-order coefficients correspond to details of the image → we can get rid of them
• JPEG (Joint Photographic Experts Group)
  • JPEG standard specifies a codec
    • lossy / lossless compression
    • progressive transmission scheme
  • file format
    • JPEG/JFIF – minimal format version
    • JPEG/Exif – digital photography
  • compression scheme
    • color space transform
      • RGB → YCbCr
      • human eye is more sensitive to details in Y (luminance) component
    • reduction of colors (chroma subsampling) in color components
      • 4:4:4 (no reduction) or 4:2:2 or 4:2:0
      • 4:2:2 or 4:2:0 → colors have lower resolution than the luminance
      • 
      • J:a:b (see Chroma subsampling, Wikipedia)
        • J … width of the region (as a reference)
        • a … number of chrominance samples in the first row
        • b … number of changes (in chrominance) between first and second row
    • each color component is handled separately
      • split into blocks of 8×8 pixels
      • DCT of each block
      • uniform quantization of DCT coefficients
        • coefficients are divided by table values (recommended in the standard, stored in the compressed file) and rounded
        • table values are adjusted according to specified JPEG quality $\in\set{1,\dots,100}$
      • coding – zigzag matrix scan, Huffman coding (extended JPEG can use arithmetic coding)
  • Huffman encoding of coefficients
    • DC coefficient encoding
      • $\theta_{11}$ = constant multiple of the average value in the block (see the image in the DCT section above)
      • instead of $\theta_{11}$ encode the difference between neighboring blocks
      • split the range of values into categories (so that the Huffman tree is not too large)
        • we output the Huffman code of the category $n$ and then $n$ bits identifying the exact value
        • values
          • category 0 … 0
          • category 1 … -1, 1
          • category 2 … -3, -2, 2, 3
          • etc.
    • AC coefficient encoding
      • the categories are the same
      • but we don't encode zeros – we use Chen & Pratt method with EOB signal
      • for each value, we need to encode its category (+ value) and the number of previous zeros
        • use Huffman tree to encode $(Z,C)$ where $Z$ is the number of previous zeros and $C$ is the category
        • append $C$ bits to store the exact value
      • if the number of previous zeros is greater than 15, use a special ZRL signal
        • ZRL is encoded as $(15,0)$
        • EOB is encoded as $(0,0)$
  • JPEG use
    • digitized images, realistic scenes, subtle variations in tone and color
    • disadvantage: artificial division into blocks → coding artifacts at the block edges → tile effect
• WebP
  • color space: RGB → YCbCr
  • chroma subsampling 4:2:0
  • split into macroblocks 16×16 Y, 8×8 Cb, 8×8 Cr
    • high detail areas: 4×4
  • macroblock prediction
  • transform: DCT, DWHT
  • quantization – partition to segments with similar features
  • arithmetic coding

Subband Coding

• example
  • rapid sample-to-sample variation
  • but the long-term trend varies slowly
  • idea: let's average the samples $x_n$ using the sliding window
    • this would smooth out the rapid variation
  • we could transmit both the averages $y_n$ and their distances $z_n$ from the original values $x_n$
    • we would need to transmit twice as many values than before
    • fortunately, if we transmit only even values, we can reconstruct the odd values from them
  • takeaway
    • it is useful to decompose original sequence $(x_n)$ into two subsequences $(y_n)$ and $(z_n)$
    • it did not result in any increase in the number of values we need to transmit
    • the two subsequences have different characteristics, we can use different techniques to encode them
• filters – selectively block frequencies that does not belong to the filtered range
  • low-pass filters – blocks frequencies above $f_0$
  • high-pass filters – block frequencies below $f_0$
  • band-pass filters – lets through only components between $f_1$ and $f_2$
• digital filter with input $(x_n)$ output $(y_n)$ coefficients $(a_i),(b_i)$
  • $y_n=\sum_{i=0}^N a_ix_{n-i}+\sum_{i=1}^Mb_iy_{n-i}$
  • finite impulse response (FIR)
    • $\forall i:b_i=0$
    • impulse response dies out after $N$ samples
    • $N$ … number of taps
  • infinite impulse response (IIR)
    • example for $a_0=1$ and $b_1=0.9$ and impulse 1000000…
      • $y_n:$ 1, 0.9, 0.81, 0.729, …
      • this $y_n$ is equal to the impulse response $h_n$
  • we can use convolution…
    • impulse response completely specifies the filter
    • $y_n=\sum_{k=0}^M h_kx_{n-k}$
    • for IIR, $M$ is infinite
  • examples of filters
    • averaging
      • low-pass filter
      • two-tap FIR filter
      • $h_n:0.5,0.5,0,\dots$
    • difference
      • high-pass filter
      • $h_n:0.5,-0.5,0,\dots$
• filters used in subband coding
  • filter bank
    • a cascade of stages
    • each stage contains low-pass and high-pass filters
  • QMF – quadrature mirror filter
    • impulse response of the low-pass filter is specified as $(h_n)$
    • impulse response of the high-pass filter is derived from that as $((-1)^nh_{N-1-n})$
      • the order is reversed and the signs are flipped
    • example: 8-tap Johnson QMF filter
    • fewer taps → lower efficiency in decomposition
• basic algorithm
  1. analysis
     • $M$ filters cover the frequency range of the input
     • generalized Nyquist rule – the sampling frequency has to be at least twice the supported frequency range
  2. downsampling (decimation)
     • keep each $M$th sample
  3. quantization + coding
     • allocation of bits between subbands
       • subband variance is a suitable heuristic
     • ADPCM, PCM, vector quantization
  4. decoding
  5. upsampling
     • insert appropriate number of zeros
  6. synthesis
     • bank of reconstruction filters
• G.722
  • ITU recommendation for speech coding
  • anti-aliasing filter with cutoff frequency 7 kHz
  • sampling frequency 16 kHz
  • 14b uniform quantizer
  • filtering – a bank of 2 QMF filters
    • 24 tap FIR filter
    • low-pass 0–4 kHz, high-pass remaining frequencies
    • down sampling by a factor of two
  • encoding – ADPCM
    • low-pass: 6b/sample
    • high-pass: 2b/sample
  • quantization – a variation of Jayant algorithm
• MPEG audio (Moving Picture Experts Group)
  • three coding schemes – layers (each is more complex than the previous)
    • MPEG-1 Audio Layer I (MP1)
    • MPEG-1 (or MPEG-2) Audio Layer II (MP2)
    • MPEG-1 (or MPEG-2) Audio Layer III (MP3)
  • subband coding
    • MP1 and MP2 use a bank of QMF filters
    • MP3 uses QMF and modified DCT
  • quantization
    • uniform (1, 2)
    • non-uniform (3)
  • bit allocation to subbands
    • based on a psychoacoustic model of human perception
    • sounds at different frequencies are perceived as differently loud even if they have the same pressure levels
    • threshold-of-hearing curve (boundary of audible sounds)
    • spectral masking
      • if there are multiple sounds of the similar frequencies, some might not be audible (audibility threshold rises)
    • temporal masking
      • sound raises the audibility threshold for a brief interval preceding and following the sound
  • coding
    • fixed codeword length (1, 2)
    • Huffman coding + a buffer to ensure fixed transmission rate (3)
• image compression
  • dependencies in two dimensions – it is better to use two one-dimensional filters rather than one two-dimensional filter
  • filter each row of an image separately using high-pass and low-pass filters, then perform downsampling by a factor of two
    • one image N×N → 2 images N×N/2
  • filter each column of the two images using high-pass and low-pass filters, then perform downsampling by a factor of two
    • 2 images N×N/2 → 4 images N/2×N/2
  • then we can stop or continue the decomposition (note: we don't have to decompose all of the subimages)
  • application: JPEG 2000
    • wavelet transform
    • coefficients correspond to details for various resolutions
      • fairly precise quantization possible
      • FBI fingerprint image compression standard, medical images compression
      • data optimization for progressive transmission over a network
      • a possibility to define regions of interest for higher-quality encoding

Video Compression

• video = time sequence of images (frames)
• can we reduce the problem to image compression?
  • no!
  • if we change the average intensity of pixels, it becomes noticeable in a video
  • on the other hand, we don't care about the reproduction of sharp edges that much
• basic types of algorithms
  • two-way communication → symmetric compression / decompression, it needs to be fast, videotelephony etc.
  • one-way → used for storage, the compression can be more complex
• video signal representation
  • CRT
  • analog TV standards: NTSC (USA), PAL (Germany), SECAM (France)
  • composite signal – YCbCr
    • Y (luminance) used for black-and-white television
  • gamma correction – to make colors look more natural
• MPEG-SIF format based on ITU-R 601 4:2:2
  • luminance compression – take odd rows, use horizontal filter and subsample (the horizontal filter prevents aliasing)
  • chrominance compression – take odd rows, use horizontal filter and subsample, use vertical filter and subsample
• ITU-R H.261
  • videotelephony, videoconferencing
  • format CIF
  • idea
    • frame = 8×8 blocks
    • prediction (by the previous frame) + differencing
    • DCT
    • quantization
    • entropy coder with variable codeword length
  • why do we have to do inverse quantization and transform when encoding?
    • to prevent loss, we need the encoding prediction to be based on the information available to the decoder (see differential encoding)
  • motion compensation
    • which parts of the image are moving?
    • for each block of the frame, we are going to find the most similar block of the previous frame
    • if there's no similar previous block, we just encode the current block
    • how to reduce the search space?
      • increase block size
    • H.261 uses macroblocks
      • for luminance component, group the blocks by four (into 16×16 macroblocks)
      • search for the best match (we get the motion vector)
      • to find the motion vector for chrominance components, we just divide the motion vector by two
  • the loop filter
    • sharp edges in the block used for prediction have some negative consequences
    • we use a smoothing filter
  • transform
    • DCT of the blocks
    • coder simulates the decoder
    • two modes
      • inter – motion compensation is used (we only have to encode the differences)
      • intra – original block is encoded directly
  • quantization
    • intra blocks have large DC coefficients, inter blocks have smaller ones
    • there are 32 different quantizers, they are identified in the macroblock header
  • coding
    • zigzag scan through the block of quantized coefficients (like in JPEG)
      • 20 most common → single variable length codeword
      • other → fixed length 20b
    • to avoid zero blocks, CBP (coded block pattern) is used to describe which blocks have non-zero coefficients
  • rate control
    • during videoconference we need the transmission rate to be steady
    • transmission buffer – keeps the output rate of the encoder fixed
      • buffer may request that the coder changes the transmission rate
      • coder than may change the quantizer (or as a last resort drop some frames)
• MPEG
  • standard describes bitstream format and decoder, not encoder
  • MPEG-1
    • lossy compression of sound and video
    • YUV color space
    • standard for video CD
    • layer 3 (MP3) format for audio compression
  • MPEG-2
    • TV broadcast, DVD
  • MPEG-3
    • originally intended for HDTV
    • development stopped, merged with MPEG-2
• MPEG-1
  • same basis as H.261
  • 8×8 blocks
  • inter/intra
  • motion-compensated prediction on macroblock level
  • DCT
  • quantization and coding
  • rate control using a transmission buffer
  • but has different applications (digital storage and retrieval)
  • frame types
    • I-frame (intraframe) – current frame (coded with no reference to other frames)
    • P-frame (predictive frame) – difference between current and most recent I/P-frame
    • B-frame (bidirectionally predictive) – difference between two closest I/P-frames (most recent and closest future frame)
    • e.g. $I:P:B \approx 2:5:12$
  • group of pictures (GOP)
    • smallest random access unit in the video sequence
    • a repeating sequence of 10–30 frames
    • contains at least one I-frame
    • starts with an I-frame or “forward-pointing” B-frames
    • usage
      • allows the video to replay at original speed even on a slow hardware
        • some frames may be skipped to keep the original speed
      • forward, jump forward/back
    • when processing a GOP, referenced frames have to be processed before the frames that reference them
  • coding
    • standard does not specify a particular method for motion compensation
      • search space size should grow with the distance between frames
    • DCT & quantization are similar to JPEG (different quantization tables for different frames)
    • rate control – we can discard B-frames first
  • properties
    • VHS quality for low-moderate motion (worse than VHS for high-motion)
    • interlacing was not considered
• MPEG-2
  • idea: application-independent standard, toolkit approach
  • profiles: simple, main, snr-scalable, spatially scalable, high
    • simple: no B-frames
    • main: like MPEG-1
  • possibility to use several layers (in the other three profiles)
    • base layer: encodes low-quality videosignal
    • enhancement layer: differential encoding to improve quality
  • several resolution levels
  • interlacing can be used
    • field-based alternatives to I/P/B-frames
    • P-frames may be replaced by 2 P-fields
    • B-frames may be replaced by 2 B-fields
    • I-frames may be replaced by 2 I-fields or I-field and P-field
      • predict the bottom field by the top field
  • new motion-compensated prediction modes
• MPEG-4
  • objective: encode video at low bitrates
  • object oriented approach: audio, video and VRML objects
  • allows to use arbitrary codecs
  • MPEG-4 Part 10 … H.264 (used in HDTV, Blu-ray)
• MPEG-M (Part 2)
  • HEVC (High Efficiency Video Coding)
  • ITU-T H.265
  • used in DVB-T2
• H.264 improvements (examples)
  • macroblocks may be further divided
  • 9 prediction models for 4×4 blocks
• H.265 improvements (examples)
  • frame is partitioned into Coded Tree Units
  • blocks can be subdivided if higher “resolution” is needed