main idea
- large set → smaller set
- quantizer can be scalar or vector
- quantization consists of two mapping – encoding and decoding
data compression
measuring the performance
limits of lossless compression
basic concepts
typical strategy
codes
prefix codes
Shannon-Fano coding
algorithm
optimality of Huffman code
idea: we could encode larger parts of the message, it might be better than Huffman coding
extended Huffman code … we use -grams instead of individual symbols
can we modify Huffman algorithm to guarantee that the resulting code minimizes the maximum codeword length?
yes, when constructing the tree, we can sort the nodes not only by their frequencies but also by the depth of their subtree
what is the maximum height of a Huffman tree for an input message of length ?
generalize the construction of binary Huffman code to the case of -ary coding alphabet ()
implementation notes
canonical Huffman code
adaptive compression
adaptive Huffman code
each string associate with a subinterval such that
encoding
decoding
problem: using floating point arithmetic leads to rounding errors → we will use integers
underflow may happen that way if we use too short integers
another problem
algorithm
time complexity
adaptive version
Hartley's formula
Shannon's formula
Kraft-McMillan theorem
proof
theorem: let be a uniquely decodable code for a random variable , then
entropy of a discrete random vector
theorem: an arbitrary optimal prefix code for a random variable satisfies
analysis of arithmetic coding
problems
a better probabilistic model
according to an experimental estimate
the entropy of English is 1.3 bits per symbol
methods
Prediction by Partial Matching (PPM)
unary code
binary code
Elias codes
Elias codes are universal
idea
problems
LZ77
ac|cabracad|abrarr|ar___\search/\lahead/__LZSS
other variants
Deflate algorithm
LZ77 disadvantages
LZ78
LZW
LZC
LZMW
LZAP
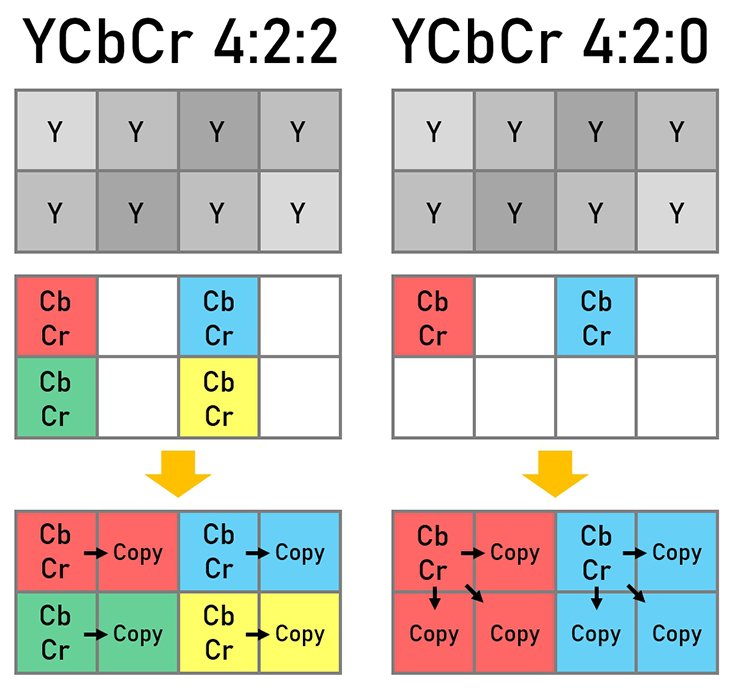
color spaces
representation of bitmap images
GIF (Graphics Interchange Format)
PNG (Portable Network Graphics)
Burrows–Wheeler transform
x$, where xis the original string and $ is a sentinel characterbzip2
how to measure the loss of information
sampling
quantization
audio processing
main idea
central limit theorem
if we collect samples of random variable , the distribution of the sample mean approaches for a sufficiently large
problem formulation
uniform quantizer
forward adaptive quantizer (offline)
backward adaptive quantizer (online)
| code | interval | multiplier |
|---|---|---|
| 0 | 0.8 | |
| 1 | 0.9 | |
| 2 | 1 | |
| 3 | 1.2 | |
| 4 | 0.8 | |
| 5 | 0.9 | |
| 6 | 1 | |
| 7 | 1.2 |
nonuniform quantization
companding
we split the file (or group the individual samples) into vectors
idea: codebook
LBG algorithm
tree-structured vector quantization (TSVQ)
lattice vector quantizers
classified vector quantization
applications
instead of that, we will quantize the difference between the previous predicted value and the current value
DPCM (differential pulse-code modulation)
ADPCM
G.726
delta modulation
↑↓↑↓↑↓↑↓)constant factor adaptive delta modulation (CFDM)
for images, we have to make a two-dimensional transform
it is better to transform each dimension separately = separable transform
separable transform using matrix
orthogonal transform … we use orthogonal transform matrix
Karhunen-Loéve transform
discrete cosine transform
discrete sine transform
gain is close to the optimum value for Markov sources with low correlation coefficient
Hadamard matrix
discrete Walsh-Hadamard transform
quantization of transform coefficients
quantization and coding
JPEG (Joint Photographic Experts Group)
WebP
example
filters – selectively block frequencies that does not belong to the filtered range
digital filter with input output coefficients
filters used in subband coding
basic algorithm
G.722
MPEG audio (Moving Picture Experts Group)
image compression
can we reduce the problem to image compression?
basic types of algorithms
video signal representation
MPEG-SIF format based on ITU-R 601 4:2:2
ITU-R H.261
MPEG
MPEG-1
MPEG-2
MPEG-4
MPEG-M (Part 2)
H.264 improvements (examples)
H.265 improvements (examples)