Základy umělé inteligence

Řešení úloh prohledáváním

• formulace úlohy
  • agent – vnímá prostředí pomocí senzorů, aktuátory mu umožňují jednat
    • racionální agent
      • zvolí akci, která maximalizuje jeho výkon
    • simple reflex agent
      • observation → action
    • model-based reflex agent
      • past state + past action + observation → state
      • state → action
    • goal-based agent
      • state + goal → action
  • reprezentace stavů agenta
    • atomic – stav je blackbox
      • dá se použít prohledávání
    • factored – stav je vektor
      • dá se použít constraint satisfaction, výroková logika, plánování
    • structured – stav je sada objektů, ty jsou propojeny
      • dá se použít (predikátová) logika prvního řádu
  • problem solving agent – typ goal-based agenta
    • atomická reprezentace stavů
    • cíl = množina cílových stavů
    • akce = přechody mezi stavy
    • hledáme posloupnost akcí, kterými se dostaneme z výchozího do nějakého cílového stavu
    • očekáváme, že prostředí je plně pozorovatelné, diskrétní, statické a deterministické
    • příklad – Lloydova patnáctka
      • ne všechny stavy jsou dosažitelné – zachovává se parita permutace
  • formulace problému
    • budeme potřebovat abstrakci prostředí (odstraníme detaily z prostředí)
      • validní abstrakce = abstraktní řešení můžeme expandovat do reálného řešení
      • užitečná abstrakce = vykonávání akcí v řešení je jednodušší než v původním problému
    • dobře definovaný problém
      • výchozí stav
      • přechodový model (state, action) -> state
      • goal test (funkce, která odpoví true/false podle toho, zda je daný stav cílový)
• stromové vs. grafové prohledávání
  • udržujeme si hranici (frontier) prozkoumané oblasti
  • graph search si navíc ukládá „uzavřenost“ vrcholu (jestli už jsme vrchol viděli)
    • takže nenastávají problémy s cykly
    • kvůli tomu, že stavový prostor může být nekonečný, neinicializujeme všechny vrcholy, ale místo toho použijeme hešovací tabulku
  • i tree search lze použít k prohledávání grafů s cykly, ale může se chovat divně
  • u prohledávání DAGů tree search nezaručuje, že se prohledané stavy nebudou opakovat (opakovat se můžou, pokud do stejného vrcholu vedou dvě orientované cesty)
• neinformované prohledávání (DFS, BFS, uniform-cost search)
  • BFS (fronta)
    • nejmělčí neexpandovaný vrchol je zvolen k expanzi
    • úplný pro konečně větvící grafy
    • optimální – pokud je cena cesty nerostoucí funkce hloubky
    • časová a prostorová složitost $O(b^{d+1})$, kde $b$ je stupeň větvení (branching factor, maximální výstupní stupeň) a $d$ je hloubka nejbližšího cíle
    • problém je s prostorovou složitostí
  • DFS (zásobník)
    • nejhlubší neexpandovaný vrchol je zvolen k expanzi
    • úplný pro graph search
      • úplný = nalezne řešení vždy, když existuje (a v opačném případě hlásí, že řešení neexistuje)
    • neúplný pro tree search (pokud algoritmus pustíme na grafu, který není strom)
    • suboptimální – nesměřuje k cíli
    • časová složitost $O(b^m)$, kde $m$ je maximální hloubka libovolného vrcholu
    • prostorová složitost $O(bm)$
    • pokud použijeme backtracking (generujeme jenom jednoho následníka místo všech), tak nám stačí dokonce jenom $O(m)$ paměti
      • DFS využívá to, že nám stav může vrátit všechny následníky (pak je držíme v paměti)
      • backtracking v daném vrcholu generuje jednoho následníka (takže všechny ostatní nemusíme držet v paměti)
        • ale někdy se nedá generovat jenom jeden následník
  • rozšíření BFS o funkci určující cenu kroku (tedy cenu hrany)
    • Dijkstrův algoritmus
    • taky se tomu říká uniform-cost search
    • $g(n)$ označuje cenu nejlevnější cesty ze startu do $n$
    • místo fronty použijeme prioritní frontu
• informované prohledávání (algoritmus A*, přípustné a konzistentní heuristiky)
  • best-first search
    • pro vrchol máme ohodnocovací funkci $f(n)$
    • $f(n)$ použijeme v Dijkstrově algoritmu místo $g(n)$
    • máme heuristickou funkci $h(n)$, která pro daný vrchol označuje odhadovanou cenu nejlevnější cesty do cílového stavu
    • best-first je třída algoritmů, kde máme uzly ohodnoceny nějakou funkcí a vybíráme nejmenší z nich
    • greedy best-first search
      • $f(n)=h(n)$
      • není optimální ani úplný
    • A* algoritmus
      • $f(n)=g(n)+h(n)$, kde $h(n)$ je heuristika
      • optimální a úplný
      • typicky mu dojde paměť dřív než čas
  • co chceme od heuristiky $h(n)$ u algoritmu A*
    • přípustnost – $h(n)$ musí být menší rovna nejkratší cestě z daného vrcholu do cíle, musí být nezáporná
    • monotónnost (= konzistence)
      • mějme vrchol $n$ a jeho souseda $n'$
      • $c(n,a,n')$ je cena přechodu z $n$ do $n'$ (akcí $a$)
      • heuristika je monotónní, když $h(n)\leq c(n,a,n')+h(n')$
    • tvrzení: monotonie implikuje přípustnost, opačná implikace neplatí
    • tvrzení: pro monotónní heuristiku jsou hodnoty $f(n)$ neklesající po libovolné cestě
    • tvrzení: pokud je $h(n)$ přípustná, pak je A* u tree search optimální
      • do cíle nevedou žádné suboptimální cesty, takže si vystačíme s důkazem optimality Dijkstrova algoritmu
    • tvrzení: pokud je $h(n)$ monotónní, pak je A* u graph search optimální
      • s nemonotónní heuristikou jsme mohli najít suboptimální cestu do cíle
  • když heuristika $h_2$ dává větší hodnoty než $h_1$, tak se říká, že $h_2$ dominuje $h_1$
    • pokud je $h_2$ přípustná a pokud se $h_2$ nepočítá výrazně déle než $h_1$, tak je $h_2$ zjevně lepší než $h_1$

Splňování omezujících podmínek

• problém splňování podmínek
  • = constraint satisfaction problem (CSP)
  • konečná množina proměnných
  • domény – konečné množiny možných hodnot pro každou proměnnou
  • konečná množina podmínek (constraints)
    • constraint je relace na podmnožině proměnných (je to podmnožina kartézského součinu domén)
    • constraint arity = počet proměnných, které podmínka omezuje
  • chceme přípustné řešení (feasible solution)
    • úplné konzistentní přiřazení hodnot proměnným
    • konzistentní … všechny podmínky jsou splněny
  • CSP můžeme řešit tree-search backtrackingem
    • úpravou proměnných v určitém pořadí můžeme získat větší efektivitu
    • můžeme pročistit hodnoty, které zjevně nesplňují podmínky
      • příklad
        • $a\in\set{3,4,5,6,7}$
        • $b\in\set{1,2,3,4,5}$
        • constraint: $a\lt b$
        • ale např. $a=6$ vůbec nedává smysl
        • odstraněním nekonzistentních hodnot dostaneme $a\in \set{3,4}$, $b\in\set{4,5}$
      • můžeme použít metodu hranové konzistence
• hranová konzistence (algoritmus AC-3)
  • = arc consistency (arc … orientovaná hrana)
  • uvažujme binární podmínky
    • libovolnou n-ární podmínku lze převést na balík binárních podmínek
  • každá binární podmínka odpovídá dvojici orientovaných hran v síti podmínek (vrcholy odpovídají proměnným)
    • pokud je mezi dvěma proměnnými více podmínek, můžeme je sloučit do jedné (abychom neměli multigraf)
  • orientovaná hrana $(V_i,V_j)$ je hranově konzistentní $\equiv$ pro každé $x\in D_i$ existuje $y\in D_j$ takové, že přiřazení $V_i=x$ a $V_j=y$ splní všechny binární podmínky pro $V_i,V_j$
    • může platit, že $(V_i,V_j)$ je hranově konzistentní, ale $(V_j,V_i)$ není
  • CSP je hranově konzistentní $\equiv$ každá hrana je hranově konzistentní (v obou směrech)
  • algoritmus AC-3
    • začínám se všemi hranami (podmínkami) ve frontě
    • postupně beru hrany z fronty a pro každou odstraním nekonzistentní prvky z domény
    • pokud jsem odstranil nějaké prvky z domény, musím zopakovat kontrolu pro hrany směřující do dané proměnné (kromě hrany opačné k té aktuálně zpracované)
    • složitost $O(cd^3)$, kde $c$ je počet podmínek, $d$ je velikost domény
      • $O(d^2)$ … kontrola konzistence
      • každá podmínka se ve frontě může objevit nejvýše $d$-krát, protože se z dané domény dá odstranit nejvýše $d$ prvků
    • optimální algoritmus má složitost $O(cd^2)$
  • hranová konzistence je typ lokální konzistence, negarantuje globální konzistenci
  • arc consistency (AC) vs. forward checking (FC)
    • FC je jednodušší (a rychlejší) než AC, slouží ke stejnému účelu – zrychlení prohledávání
    • FC na základě přiřazení do proměnné (v daném kroku prohledávání) pročistí domény dosud nepřiřazených proměnných
    • AC k tomu navíc zajišťuje vzájemnou kompatibilitu domén nepřiřazených proměnných
• algoritmus hledání řešení (MAC)
  • chceme zkombinovat AC a backtracking
  • problém uděláme hranově konzistentní
  • po každém přiřazení obnovíme hranovou konzistenci
  • této technice se říká look ahead nebo constraint propagation nebo udržování hranové konzistence (MAC, maintaining arc consistency)
  • kontroly FC/AC jsou v polynomiálním čase, kdežto strom stavů se větví exponenciálně

Logické uvažování

• základy výrokové logiky (konjunktivní a disjunktivní normální forma)
  • viz Společná matematika
  • výrokovou logiku lze použít k logickému odvozování znalostí na základě znalostní báze
• algoritmus DPLL
  • literál $\ell$ má čistý výskyt ve $\varphi$, pokud se $\ell$ vyskytuje ve $\varphi$ a opačný literál $\overline\ell$ se ve $\varphi$ nevyskytuje
    • takový literál můžu nastavit na 1
    • to neovlivní splnitelnost výroku, ale zmenší to množinu modelů, které jsem schopen nalézt
  • algoritmus
    • dokud $\varphi$ obsahuje jednotkovou klauzuli $\ell$, ohodnoť $\ell=1$ a proveď jednotkovou propagaci
      • každou klauzuli obsahující $\ell$ odstraníme (protože je takto splněna)
      • $\overline\ell$ odstraníme ze všech klauzulí, které ho obsahují (protože $\overline\ell$ nemůže zajistit splnění dané klauzule)
    • dokud existuje literál $\ell$, který má ve $\varphi$ čistý výskyt, ohodnoť $\ell=1$ a odstraň klauzule obsahující $\ell$
    • pokud $\varphi$ neobsahuje žádnou klauzuli, je splnitelný
    • pokud $\varphi$ obsahuje prázdnou klauzuli, není splnitelný
    • jinak zvol dosud neohodnocenou výrokovou proměnnou $p$ a zavolej algoritmus rekurzivně na $\varphi\land p$ a na $\varphi\land\neg p$
  • algoritmus běží v exponenciálním čase
  • praktické poznámky
    • čistý výskyt se zas tak moc nepoužívá
    • jednotková propagace
      • hledám klauzule o jedné proměnné
      • je v zásadě ekvivalentní hranové konzistenci
    • ke zkoušení hodnot proměnných se používá tree search
• dopředné a zpětné řetězení (Hornovské klauzule)
  • mám dotaz $\alpha$, ten vyjádřím jako výrokovou formuli
    • znalostní bázi $KB$ vyjádřím jako teorii
    • zajímá mě, zda $KB\models\alpha$ (to platí, právě když $KB\land\neg\alpha$ je nesplnitelné)
  • řetězení můžeme použít, pokud znalostní báze obsahuje pouze Hornovy klauzule
    • Hornova klauzule = disjunkce literálů, z nichž nejvýše jeden je pozitivní
    • Hornovu klauzuli $\neg p\lor\neg q\lor\neg r\lor s$ lze zapsat jako implikaci $p\land q\land r\implies s$
  • forward chaining … data-driven reasoning
    • $p\land q\land r\implies s$
    • pokud vím, že platí $p$, pak převedu na $q\land r\implies s$
    • jakmile se počet předpokladů sníží na 0, vím, že $s$ platí
    • je to v podstatě speciální případ použití rezolučního pravidla
      • rezolvuju to, co vím, s libovolnou klauzulí
    • algoritmus
      • každá proměnná má počítadlo proměnných, které na ni ukazují
      • postupně beru pravdivé proměnné, snižuju počítadla u proměnných, na které ukazují
      • jakmile u proměnné klesne počítadlo na nulu, zařadím mezi pravdivé proměnné
  • backward chaining … goal-driven reasoning
    • něco mě zajímá – pokouším se to odvodit
      • najdu klauzule, kde je nějaký literál z $\alpha$ na pravé straně implikace
      • tak dostanu další literály, které musím dokázat
      • postupuju tak dlouho, dokud se nedostanu k faktům (literálům, o nichž vím, že platí)
    • tohle se používá v Prologu
    • opět vlastně používám rezoluční pravidlo
      • to, co chci zjistit, rezolvuju s libovolnou klauzulí
  • forward chaining prochází spoustu klauzulí, které nás nezajímají – backward chaining může mít výrazně menší složitost
• rezoluce
  • mám dotaz $\alpha$, ten vyjádřím jako výrokovou formuli
    • znalostní bázi $KB$ vyjádřím jako teorii
    • zajímá mě, zda $KB\models\alpha$ (to platí, právě když $KB\land\neg\alpha$ je nesplnitelné)
  • $KB\land\neg\alpha$ převedeme do CNF → dostaneme množinu klauzulí (formuli $S$)
  • použijeme rezoluci (zkonstruujeme rezoluční zamítnutí formule $S$)
    • použitím rezolučního pravidla z klauzulí $\varphi\lor p$ a $\psi\lor\neg p$ dostaneme $\varphi\lor\psi$
    • zkoušíme spolu rezolvovat postupně všechny dvojice klauzulí
    • pokud v průběhu dostaneme prázdnou klauzuli, máme rezoluční důkaz $\alpha$ z $KB$
    • pokud se dostaneme do stavu, kdy nelze použít rezoluční pravidlo na žádnou dvojici klauzulí, tak víme, že neplatí $KB\models\alpha$

Pravděpodobnostní uvažování

• základy teorie pravděpodobnosti (úplná sdružená distribuce, nezávislost, Bayesovo pravidlo)
  • viz Společná matematika
  • pravděpodobnostní uvažování umožňuje agentovi zacházet s nejistotou
  • zdroji nejistoty jsou částečná pozorovatelnost (nelze snadno zjistit současný stav) a nedeterminismus (není jisté, jak akce dopadne)
  • agent si pamatuje belief state – pravděpodobnostní distribuce přes všechny možné stavy světa, v nichž se agent může nacházet
• pravděpodobnostní uvažování (vysčítání, normalizace)
  • někdy si můžeme udělat tabulku všech možností a určit jejich pravděpodobnosti (full joint probability distribution)
    • odpověď lze vyjádřit z ní (této metodě se říká enumeration, výčet) – ale u velkých tabulek je někdy potřeba posčítat příliš mnoho hodnot
  • $P(Y)=\sum_z P(Y\mid z)\cdot P(z)$
  • $P(Y\mid e)=\frac{P(Y\land e)}{P(e)}$
    • typicky nemusíme znát $P(e)$, stačí použít $\alpha P(Y\land e)$, kde $\alpha$ je normalizační konstanta
  • velkou tabulku můžeme někdy reprezentovat menším způsobem – pokud jsou proměnné podmíněně nezávislé
  • Bayesovo pravidlo … $P(Y\mid X)=\frac{P(X\mid Y)P(Y)}{P(X)}=\alpha P(X\mid Y) P(Y)$
    • lze odvodit z definice podmíněné pravděpodobnosti
    • pomůže nám při přechodu z příčinného k diagnostickému směru
      • $P(\mathrm{effect} \mid \mathrm{cause})$ … casual direction (příčinný směr), obvykle známý
      • $P(\mathrm{cause} \mid \mathrm{effect})$ … diagnostic direction (diagnostický směr), obvykle chceme zjistit
      • známe důsledky; chceme zjistit, jaké příčiny k nim mohly vést
  • naivní bayesovský model
    • $P(\text{Cause}, \text{Effect}_1, \dots, \text{Effect}_n) = P(\text{Cause})\prod_iP(\text{Effect}_i\mid\text{Cause})$
    • předpokládáme nezávislost důsledků
  • chain rule
    • $P(x_1,\dots,x_n)=\prod_iP(x_i\mid x_{i-1},\dots,x_1)$
    • využívá product rule (lze odvodit z definice podmíněné pravděpodobnosti)
• Bayesovské sítě: konstrukce a vztah k úplné sdružené distribuci
  • bayesovská síť je DAG, kde vrcholy odpovídají náhodným proměnným
    • šipky popisují závislost
    • u každého vrcholu jsou CPD tabulky, které popisujou jeho závislost na rodičích
      • CPD = conditional probability distribution
      • pro každou kombinaci hodnot rodičů jsou v CPD tabulce pravděpodobnosti hodnot dané náhodné proměnné
  • 
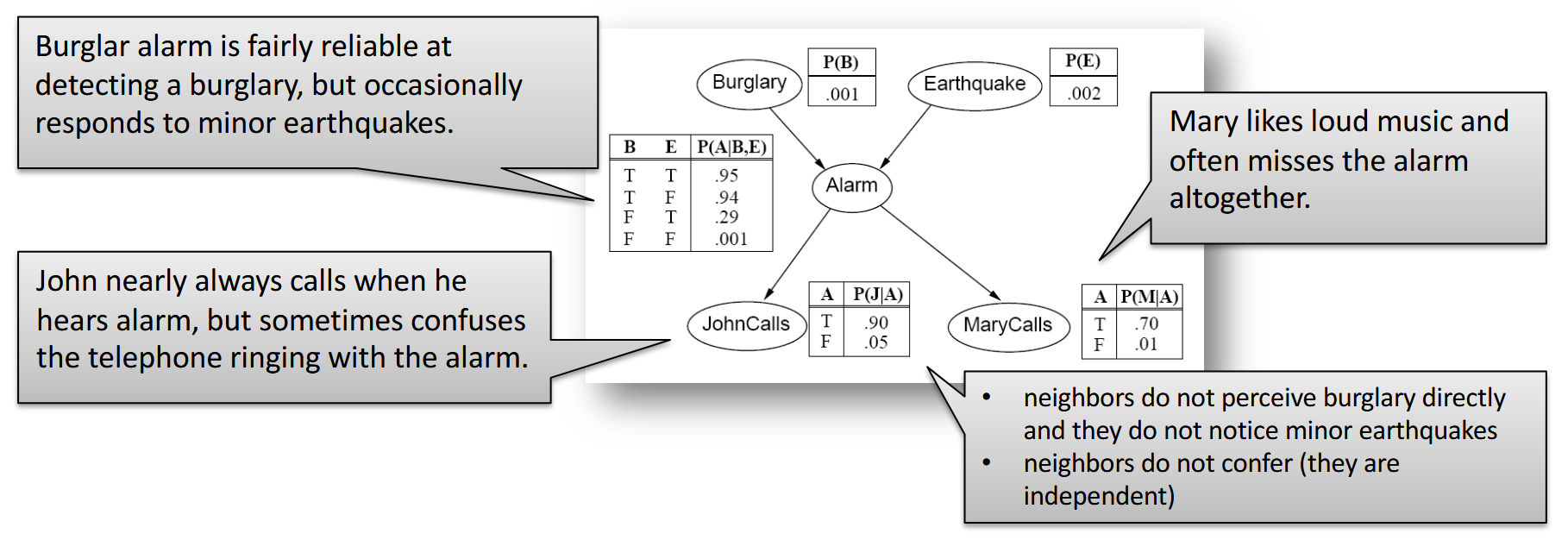
    • autorem obrázku je Roman Barták
    • proměnné jsou binární, proto má tabulka vždy jen jeden sloupec (druhý sloupec by mohl obsahovat pravděpodobnost, že jev nenastane – lze ho dopočítat z prvního sloupce)
  • konstrukce bayesovské sítě
    • nějak si uspořádáme proměnné
      • lepší je řadit je od příčin k důsledkům – budeme mít menší síť a CPD tabulky se nám budou vyplňovat snáze
    • jdeme odshora dolů, přidáváme správné hrany
    • příklad: MaryCalls, JohnCalls, Alarm, Burglary, Earthquake (záměrně jdeme od důsledků k příčinám, byť to není praktické)
      • z MaryCalls povede hrana do JohnCalls, protože nejsou nezávislé (když volá Mary, tak je větší šance, že volá i John)
      • z obou povede hrana do Alarmu
      • z Alarmu vedou hrany do Burglary a Earthquake (ale hrany z JohnCalls a MarryCalls tam nepovedou – na těch hranách nezáleží, jsou nezávislé)
      • z Burglary povede hrana do Earthquake, protože pokud zní alarm a k vloupání nedošlo, tak pravděpodobně došlo k zemětřesení
      • akorát se nám v tomto pořadí budou špatně určovat CPD
  • bayesovská síť zachycuje úplnou sdruženou (joint) distribuci
    • dokážeme určit pravděpodobnost libovolné kombinace hodnot náhodných proměnných
    • pronásobíme mezi sebou hodnoty z tabulek
• Bayesovské sítě: exaktní odvozování (enumerace, eliminace proměnných)
  • z bayesovských sítí můžeme provádět inferenci – odvozovat pravděpodobnost proměnných pomocí pravděpodobností skrytých proměnných
  • $P(X\mid e)=\alpha P(X,e)=\alpha\sum_y P(X,e,y)$
    • kde pravděpodobnost $X$ odvozujeme, $e$ jsou pozorované proměnné (evidence) a $y$ jsou hodnoty další skryté proměnné $Y$
  • přičemž $P(X,e,y)$ lze určit pomocí CPD tabulek
    • když nemůžeme určit konkrétní hodnotu pravděpodobnosti přímo, tak výpočet rozvětvíme
    • některé větve se objeví vícekrát – hodí se nám dynamické programování
  • používáme faktory (tabulky odpovídající CPD tabulkám)
    • tabulky s faktory mezi sebou můžeme násobit
    • eliminace
      • mějme faktor s pravděpodobnostmi $P(A,B,C)$ pro všechny možné kombinace hodnot proměnných
      • můžeme ho rozdělit na dvě půlky (v jedné bude všude platit $A$, v druhé $\neg A$)
      • tyhle dvě půlky můžeme sečíst (vždy odpovídající řádky)
      • tak eliminujeme proměnnou $A$, dostaneme faktor s pravděpodobnostmi $P(B,C)$
• Bayesovské sítě: aproximační odvozování (Monte Carlo, zamítání, vážení věrohodností)
  • odhadujeme hodnoty, které je těžké přímo spočítat
    • třeba když je síť moc velká a hustě propojená
    • zajímá nás $P(X\mid e)$
  • generujeme hodně vzorků, použijeme statistiku
  • pravděpodobnostní rozdělení náhodných veličin známe (postupujeme topologicky bayesovskou sítí a generujeme hodnoty)
  • jak generovat vzorky?
    • rejection sampling = zahodíme vzorky, kde neplatí $e$
      • odhadneme $P(X\mid e)\approx\frac{N(X,e)}{N(e)}$
        • $N(X,e)$ … počet vzorků, kde platí $X,e$
      • riziko, že zahodíme příliš mnoho vzorků
    • likelihood weighting
      • zafixujeme (ignorujeme) $e$, generujeme jen zbylé proměnné
      • počtům $N$ přidělíme váhy podle pravděpodobnosti $e$ (např. místo toho, abychom zahodili cca 90 % vzorků, přiřadíme těm počtům váhu 0.1)
      • problém nastává, když jsou váhy příliš malé

Reprezentace znalostí

• situační kalkulus, problém rámce
  • problém rámce
    • návrh: stav světa/agenta budeme popisovat pomocí časově anotovaných výrokových proměnných
    • musíme definovat spoustu axiomů, které zajistí, že se hodnoty proměnných mezi časovými kroky nemění náhodně
    • tak bychom snadno zahltili odvození pomocí výrokové logiky, protože bychom měli hodně akcí a stavů
  • jak předejít opakování axiomů pro různé časy a podobné akce?
    • použijeme predikátovou logiku prvního řádu (situation calculus)
    • náš modelovaný svět se vyvíjí – postupně nastávají různé situace
      • úvodní situace … $s_0$
      • situace po aplikace akce $a$ na situaci $s$ … $\text{Results}(s,a)$
    • stavy jsou definovány jako relace mezi objekty
      • pokud se relace mění, musíme přidat další argument označující situaci, v níž relace platí: $\mathrm{at}(\mathrm{robot}, \mathrm{location}, s)$
      • pro stálé relace takový argument není potřeba: $\mathrm{connected}(l, l')$
    • podmínky (předpoklady) akcí jsou definovány possibility axiomem
      • obecný tvar: $\varphi(s)\implies \text{Poss}(a,s)$
        • kde $\varphi$ je formule popisující předpoklady akce $a$
      • např. $\mathrm{at}(a, l, s) \land \mathrm{connected}(l, l') \implies \mathrm{Poss}(\mathrm{go}(a, l, l'), s)$
    • vlastnosti dalšího stavu jsou popsány pomocí successor-state axiomů
      • např. $\mathrm{Poss}(a, s) \implies$ $(\mathrm{at}(a,y,\mathrm{Results}(s, a)) \iff a=\mathrm{go}(a,x,y) \lor (\mathrm{at}(a,y,s) \land a\neq \mathrm{go}(a,y,z))$
    • plánování se provádí tak, že se zeptáme, zda existuje situace, kde je cílová podmínka pravdivá
• Markovské modely – filtrace, predikce, vyhlazování, nejpravděpodobnější průchod
  • každý stav světa je popsán množinou náhodných proměnných
    • skryté náhodné proměnné $X_t$ – popisují reálný stav
    • pozorovatelné náhodné proměnné $e_t$ – popisují, co pozorujeme
    • uvažujeme diskrétní čas, takže $t$ označuje konkrétní okamžik
    • množinu proměnných od $X_a$ do $X_b$ budeme značit jako $X_{a:b}$
  • formální model
    • skrytý Markovův model (HMM) je dvojice $(X_n,e_n)$
      • $X_n$ a $e_n$ jsou náhodné (stochastické) procesy, takže vlastně posloupnosti náhodných proměnných
      • $X_n$ je markovský proces, který nemůžeme přímo pozorovat
    • transition model
      • určuje pravděpodobnostní rozložení proměnných posledního stavu, když známe jejich předchozí hodnoty … $P(X_t\mid X_{0:t-1})$
      • zjednodušující předpoklady
        • další stav závisí jen na předchozím stavu … Markov assumption
        • všechny přechodové tabulky $P(X_t\mid X_{t-1})$ jsou identické přes všechna $t$ … stationary process
    • sensor (observation) model
      • popisuje, jak pozorované proměnné závisí na ostatních proměnných … $P(e_t\mid X_{0:t},e_{1:t-1})$
      • zjednodušující předpoklad: pozorování záleží jen na aktuálním stavu … sensor Markov assumption
  • základní inferenční úlohy
    • filtrování – znám minulá pozorování, zajímá mě přítomný stav
      • $P(X_{t+1}\mid e_{1:t+1})=P(X_{t+1}\mid e_{1:t},e_{t+1})$
        • použijeme Bayesovo pravidlo
      • $=\alpha\cdot P(e_{t+1}\mid X_{t+1},e_{1:t})\cdot P(X_{t+1}\mid e_{1:t})$
        • použijeme sensor Markov assumption
      • $=\alpha\cdot P(e_{t+1}\mid X_{t+1})\cdot P(X_{t+1}\mid e_{1:t})$
      • $=\alpha\cdot P(e_{t+1}\mid X_{t+1})\cdot \sum_{x_t}P(X_{t+1}\mid x_t,e_{1:t})\cdot P(x_t\mid e_{1:t})$
      • $=\alpha\cdot P(e_{t+1}\mid X_{t+1})\cdot \sum_{x_t}P(X_{t+1}\mid x_t)\cdot P(x_t\mid e_{1:t})$
      • užitečný filtrovací algoritmus si musí udržovat odhad současného stavu, jelikož je vzorec rekurzivní
      • používá se forward algoritmus
    • předpověď (prediction) – znám minulá pozorování, zajímají mě budoucí stavy
      • vlastně jako filtering, akorát nepřidávám další pozorování (měření)
      • $P(X_{t+k+1}\mid e_{1:t})=\sum_{x_{t+k}} P(X_{t+k+1}\mid x_{t+k})\cdot P(x_{t+k}\mid e_{1:t})$
      • po určitém čase (mixing time) distribuce předpovědí konverguje ke stacionárnímu rozdělení daného markovského procesu a zůstane konstantní
    • vyhlazování (smoothing) – znám minulá pozorování, zajímají mě minulé stavy
      • $P(X_k\mid e_{1:t})=P(X_k\mid e_{1:k},e_{k+1:t})$
        • použijeme Bayesovo pravidlo
      • $=\alpha\cdot P(X_k\mid e_{1:k})\cdot P(e_{k+1:t}\mid X_k,e_{1:k})$
        • použijeme sensor Markov assumption
      • $=\alpha\cdot P(X_k\mid e_{1:k})\cdot P(e_{k+1:t}\mid X_k)$
      • přitom levý člen známe z filteringu (je to „dopředný směr“), pravý je „zpětný směr“ z naměřených hodnot v budoucnosti (relativně vůči danému okamžiku)
      • používá se forward-backward algoritmus
    • nejpravděpodobnější vysvětlení (most likely explanation) – znám minulá pozorování, zajímá mě nejpravděpodobnější posloupnost minulých stavů
      • hledáme posloupnost $X_{1:t}$ takovou, že má největší $P(X_{1:t+1}\mid e_{1:t+1})$
      • opět existuje rekurzivní vzorec – podíváme se na pravděpodobnosti předchozích stavů a na nejpravděpodobnější „cesty“ do těchto stavů
      • používá se Viterbiho algoritmus
• skryté Markovské modely (HMM) vs. dynamické Bayesovské sítě
  • skryté Markovovy modely
    • předpokládejme, že stav procesu je popsán jedinou diskrétní náhodnou proměnnou $X_t$ (a máme jednu proměnnou $E_t$ odpovídající pozorování)
    • pak můžeme všechny základní algoritmy (filtering, prediction, smoothing, …) implementovat maticově
  • dynamická bayesovská síť
    • umožňuje popsat víc náhodných proměnných
    • reprezentuje časový pravděpodobnostní model
    • zachycuje vztah mezi minulým a současným časovým okamžikem (minulou a současnou vrstvou)
    • každá stavová proměnná má rodiče ve stejné vrstvě nebo v předchozí (podle Markovova předpokladu)
  • dynamická bayesovská síť (DBN) vs. skrytý Markovův model (HMM)
    • skrytý Markovův model je speciální případ dynamické bayesovské sítě
    • dynamická bayesovská síť může být kódovaná jako skrytý Markovův model
      • jedna náhodná proměnná ve skrytém Markovově modelu je n-tice hodnot stavových proměnných v dynamické bayesovské síti
      • v HMM vlastně celý stav světa komprimujeme do jedné náhodné proměnné – v DBN jich můžeme mít víc
    • vztah mezi DBN a HMM je podobný jako vztah mezi běžnými bayesovskými sítěmi a tabulkou s full joint probability distribution
      • DBN je úspornější

Automatické plánování

• formulace plánovacího problému (definice operátoru)
  • stav světa je reprezentován jako množina proměnných
    • stav je popsán atomy, které platí (ostatní neplatí, používáme předpoklad uzavřeného světa)
    • pravdivnostní hodnota některých atomů se mění … fluents
    • u jiných atomů je pravdivostní hodnota stálá … rigid atoms
  • schémata akcí (operátory) popisují možnosti agenta
    • schéma akce (operátor) popisuje akci, aniž by specifikovalo objekty, na které se akce vztahuje
    • operátor je trojice (název, předpoklady, důsledky)
      • název – obsahuje rovněž parametry operátoru (proměnné, které se objevují v předpokladech a důsledcích)
      • předpoklady – musí platit v daném stavu, aby se operátor dal použít
      • důsledky – literály (fluenty!), které budou platit, jakmile se operátor provede
    • akce je plně zinstanciovaný operátor (za proměnné jsme dosadili konstanty)
    • akce je relevantní pro cíl $g\equiv$ přispívá cíli $g$ a její důsledky (efekty) nejsou v konfliktu s $g$
    • dále definujeme výsledek aplikace akce na stav a regresní množinu pro cíl a akci
  • terminologie
    • popisu operátorů se obvykle říká doménový model
    • plánovací problém je trojice $(O,s_0,g)$, kde $O$ je doménový model, $s_0$ je výchozí stav a $g$ je cílová podmínka
    • plán je posloupnost akcí
  • plánování je realizováno prohledáváním stavového prostoru
    • ten je mnohdy dost velký
• dopředné a zpětné plánování
  • forward (progression) planning
    • postupujeme od výchozího k cílovému stavu
    • prohledávací algoritmus potřebuje dobrou heuristiku
  • backward (regression) planning
    • prozkoumávají se jen relevantní akce → menší větvení než u forward planningu
    • používá množiny stavů spíše než individuální stavy → je těžké najít dobrou heuristiku

Markovské rozhodovací procesy (MDP)

• formulace problému (výpočet užitku, strategie)
  • řešíme sekvenční rozhodovací problém
  • pro plně pozorovatelné stochastické (nedeterministické) prostředí
  • máme Markovův přechodový model a reward
    • přechodový model $P(s'\mid s,a)$ … pravděpodobnost dosažení stavu $s'$, když ve stavu $s$ použiju akci $a\in A(s)$
    • odměna (reward) $R(s)$ … získá ji agent ve stavu $s$, je krátkodobá
    • utility function $U([s_0,s_1,s_2,\dots])=R(s_0)+\gamma R(s_1)+\gamma^2 R(s_2)+\dots$
      • kde $\gamma$ je discount factor, číslo mezi 0 a 1
        • jak moc si ceníme budoucích odměn
      • utility je „dlouhodobá lokální odměna“
      • hodnota utility funkce je konečná i pro nekonečnou posloupnost stavů, protože zjevně $U([s_0,\dots])\leq \frac{R_\text{max}}{1-\gamma}$
  • řešením MDP je policy (strategie) – funkce doporučující akci pro každý stav
    • tzn. strategie je zobrazení $\pi:S\to A$
    • potřebujeme zobrazení, protože kdyby řešením byla fixní sekvence akcí, tak by to nefungovalo pro stochastická prostředí (mohlo by se stát, že skončíme v jiném stavu, než jsme mysleli)
    • optimální strategie $\equiv$ strategie, která vrací největší střední hodnotu užitku (utility)
    • optimální strategie nezávisí na počátečním stavu – je jedno, kde jsme začali, pro nalezení nejvhodnější další akce by měl být důležitý jen aktuální stav
• Bellmanova rovnice
  • opravdový užitek stavu je reward (odměna) stavu ve spojení se střední hodnotou užitku následného stavu → to vede na Bellmanovu rovnici
  • vezmu reward a discountovaný užitek okolí
  • akorát nevím, kterou akci provedu, tak vezmu všechny a maximum přes ně (násobím jejich užitek pravděpodobností)
  • $U(s)=R(s)+\gamma\max_a\sum_{s'}P(s'\mid s,a)\cdot U(s')$
• iterace hodnot, iterace strategií
  • předpoklad: známe reward $R$ a transition model $P$
    • chceme najít užitek $U$ nebo optimální strategii $\pi$
  • soustava Bellmanových rovnic není lineární – obsahuje maximum
    • můžeme je řešit aproximací
    • použijeme iterativní přístup
      • nastavíme nějak užitky – třeba jako nuly
      • provedeme update – aplikujeme Bellmanovu rovnici
      • iterujeme, dokud to nezkonverguje
    • → value iteration
  • strategie se ustálí dřív než užitky
    • policy loss … vzdálenost mezi optimálním užitkem a užitkem strategie
    • můžeme iterativně zlepšovat policy, dokud to jde
    • → policy iteration
    • z rovnic nám zmizí maximum → máme lineární rovnice
      • policy evaluation = nalezení řešení těchto rovnic (tak najdeme utilities stavů)
      • gaussovka je $O(n^3)$
      • u velkých stavových prostorů dává smysl k policy evaluation použít value iteration
    • algoritmus doběhne, protože policies je jenom konečně mnoho a vždycky hledáme tu lepší
• POMDP (základní definice)
  • máme přechodový model $P(s'\mid s,a)$, akce $A(s)$ i odměny $R(s)$
  • navíc nám přibude sensor model $P(s\mid e)$
  • místo reálných stavů můžeme používat ty domnělé (belief states)
  • modely přechodů a senzorů jsou reprezentovány dynamickou bayesovskou sítí
  • přidáme rozhodování a užitky, čímž dostaneme dynamickou rozhodovací síť
  • generujeme si stromeček, kde se střídají vrstvy akcí a belief states
  • používá se algoritmus podobný algoritmu expected minimax

Hry a teorie her

• algoritmy Minimax a alfa-beta prořezávání
  • algoritmus minimax umožňuje u hry dvou hráčů s nulovým součtem a s úplnou informací určit optimální strategie obou hráčů
    • procházíme strom hry
    • v listech nebo v určité hloubce získáme ohodnocení vrcholů
      • omezení hloubky je důležité zvláště u her, jejichž stromy se hodně větví – je potřeba zvolit vhodný přístup k ohodnocení konkrétní herní situace
    • následně vždy v rodiči zvolíme minimum nebo maximum ze synů (v závislosti na tom, který hráč je zrovna na tahu – volba minima a maxima se střídají stejně jako tahy hráčů)
    • takto pro každý vrchol určíme, jaký tah je v dané situaci optimální
      • za předpokladu, že protihráč hraje optimálně – což je nejhorší možný scénář
  • alfa-beta prořezávání
    • je to rozšíření minimaxu, které může zrychlit jeho běh tak, že omezuje počet větví, které je potřeba projít a vyhodnotit
    • vycházíme z následujícího pozorování
      • v algoritmu typicky hledáme maximum z několika hodnot, které jsou minimy (nebo naopak)
      • v určitém vrcholu máme seznam doposud určených minim z jednotlivých větví (z nich je nějaké maximální)
      • snažíme se určit další minimum, na základě jedné z podvětví máme nějaké prozatímní minimum (museli bychom projít další podvětve pod daným vrcholem, abychom dostali výsledné minimum)
      • pokud je tohle prozatímní minimum menší než prozatímní maximum (ve vyšší úrovni), tak už ty další větve nemusíme procházet, protože výsledné minimum nemůže být větší než prozatímní minimum
    • alfa-beta prořezávání nemá vliv na výsledek algoritmu
    • záleží na pořadí, ve kterém tahy (větve) procházíme
    • minimax se obvykle používá rekurzivně, meze určující prořezávání (pro jednoho hráče je to maximum, pro druhého minimum) se do funkce předávají jako parametry alfa a beta
• základy teorie her (vězňovo dilema, Nashovo ekvilibrium)
  • jednou z úloh teorie her je volba vhodné strategie – tedy návodu, jak hru hrát
    • uvažujeme hry v normálním tvaru: hru tvoří hráči, jejich akce a užitkové funkce
    • hráči táhnou zároveň, každý provede jedinou akci
    • strategie může být čistá (přímo konkrétní akce) nebo smíšená (pravděpodobnostní rozdělení přes akce)
  • díváme se na optimalitu strategie nebo strategického profilu (množiny strategií všech hráčů) z různých úhlů pohledu
    • strategie $s_1$ dominuje strategii $s_2$, pokud při volbě $s_1$ získá hráč větší užitek než při volbě $s_2$ nehledě na strategie ostatních hráčů
      • strategie je dominantní, pokud dominuje všechny ostatní strategie
    • Nashovo ekvilibrium je takový strategický profil, že by žádný hráč neměnil svou strategii, kdyby znal strategie ostatních
    • strategický profil $s$ Pareto dominuje profil $s'$, pokud si změnou z $s'$ na $s$ žádný hráč nepohorší, ale aspoň jeden hráč si polepší
      • strategický profil je Pareto optimální, pokud neexistuje profil, který by ho Pareto dominoval
    • další zajímavým typem ekvilibria je korelované ekvilibrium
  • vězňovo dilema
    • dva hráči (vězni)
    • vězeň může vypovídat (testify/defect) nebo odmítnout vypovídat (refuse/cooperate)
      • oba vypovídají → oba ztrácejí málo (užitek -5)
      • jeden vypovídá, druhý ne → jeden neztratí nic (užitek 0), druhý hodně ztratí (užitek -10)
      • oba odmítnou → oba ztrácejí velmi málo (užitek -1)
    • vypovídat je čistá dominantní strategie
      • ale když vypovídají oba hráči, tak vyhrála policie – lepší by bylo, kdyby oba odmítli vypovídat
      • našli jsme Nashovo ekvilibrium – nikdo neprofituje ze změny strategie, pokud druhý hráč zůstane u stejné strategie
• mechanism design (typy aukcí)
  • jak se pozná dobrý mechanismus aukce
    • maximalizuje výnos pro prodejce
    • vítěz aukce je agent, který si věci nejvíc cení
    • zájemci by měli mít dominantní strategii
  • anglická aukce (ascending-bid)
    • začnu s $b_\text{min}$, pokud je to nějaký zájemce ochotný zaplatit, tak se ptám na $b_\text{min}+d$
    • strategie: přihazuju, dokud cena není vyšší než moje hodnota
      • dominantní strategie
  • holandská aukce
    • začíná se vyšší cenou, snižuje se, dokud ji někdo nepřijme
  • obálková aukce
    • největší nabídka vítězí
    • neexistuje dominantní strategie
      • pokud věříš, že maximum ostatních nabídek je $b_0$, tak bys měl nabídnout $b_0+\varepsilon$, pokud je to menší částka než hodnota, kterou pro tebe věc má
  • obálková second-price aukce (Vickrey)
    • vyhraje ten, kdo nabídne nejvyšší cenu, platí druhou nejvyšší nabídnutou cenu
    • dominantní strategie je tam dát svoji hodnotu
  • VCG mechanismus
    • lze použít při obecnějších (víceparametrických) aukcích

Strojové učení

• základní druhy učení (s učitelem, bez učitele, zpětnovazební)
  • učení bez učitele (unsupervised learning) – agent se učí vzory ve vstupu, aniž by měl nějakou explicitní zpětnou vazbu
  • zpětnovazební učení (reinforcement learning) – agent dostává odměny nebo tresty podle toho, jak se chová v prostředí
  • učení s učitelem (supervised learning) – agent se učí funkci, která mapuje vstupy na výstupy
• rozhodovací stromy (definice, konstrukce)
  • přijímá vektor hodnot atributů, vrací výslednou hodnotu
  • na základě tabulky příkladů se dá postavit strom
    • každý vnitřní vrchol odpovídá testu jednoho atributu
    • dá se zjistit odůvodnění konkrétního rozhodnutí
    • strom se dá postavit hladovou metodou rozděl a panuj
      • k dělení se používá entropie
    • každý list určuje hodnotu, kterou klasifikační funkce vrátí
• regrese, SVM (základní principy)
  • při regresi přiřazujeme položce $x$ vhodnou funkční hodnotu $y$
    • je to jedna z úloh strojového učení s učitelem
  • support-vector machine (SVM)
    • stojí na lineární regresi
    • pokud lze třídy oddělit nadrovinou, zvolí takovou, která je nejdál od všech dat (příkladů)
    • nadrovina … maximum margin separator
    • pokud nejde použít nadrovinu, provede mapování do vícedimenzionálního prostoru (pomocí kernel function), kde už příklady půjde oddělit
    • SVMs jsou neparametrická metoda – příklady blíže k separátoru jsou důležitější, říká se jim support vectors (vlastně definují ten separátor)
• Bayesovské učení, EM algoritmus
  • bayesovské učení
    • máme několik hypotéz
    • na základě pozorování upravujeme jejich pravděpodobnost
    • maximálně věrohodná hypotéza
      • z množiny hypotéz je to ta, která přiřazuje naměřeným datům největší pravděpodobnost
      • $\mathrm{argmax}_h\,p(\mathrm{data}\mid h)$ nebo také $\mathrm{argmax}_h\,p_h(\mathrm{data})$
      • pokud je hypotéza parametrizovaná (hledáme parametr), tak můžeme hledat hodnotu parametru, pro níž je derivace logaritmu pravděpodobnosti nulová
        • tomu se říká maximum-likelihood parameter learning
    • z $p(\mathrm{data}\mid h)$ můžeme získat $p(h\mid\mathrm{data})=\frac{p(\mathrm{data}\mid h)p(h)}{\sum_{h'} p(\mathrm{data}\mid h')p(h')}$
      • pokud mají všechny hypotézy stejné apriorní pravděpodobnosti, stačí vzít $p(\mathrm{data}\mid h)$ a normalizovat je, jelikož $\frac{p(h)}{\sum_{h'} p(\mathrm{data}\mid h')p(h')}$ bude konstantní
    • bayesovsky optimální predikce pravděpodobnosti pro vstupní data a konkrétní predikci $z$
      • $p(z\mid\mathrm{data})=\sum_h p(z\mid h)\cdot p(h\mid\mathrm{data})$
  • algoritmus expectation-maximization (EM)
    • používá se k maximum-likelihood odhadu, pokud se nedá jednoduše spočítat
    • předstíráme, že známe parametry modelu (na začátku je určíme náhodně)
    • iterujeme dva kroky (dokud to nezkonverguje)
      • dopočteme střední hodnoty skrytých proměnných (E-step, expectation)
      • upravíme parametry, abychom maximalizovali likelihood modelu (M-step, maximization)
    • příklad
      • chceme odhadnout průměrnou výšku mužů a žen
      • máme data o naměřených výškách, ale chybí nám údaje o pohlaví (zda je to výška muže nebo ženy)
        • třídy označíme jako 0 (muži), 1 (ženy)
      • začneme tak, že oba parametry (průměrná výška mužů $\mu_0$, průměrná výška žen $\mu_1$) inicializujeme náhodně
      • v E-kroku spočítáme střední hodnoty skrytých proměnných
        • pohlaví je skrytá proměnná (pro každou naměřenou výšku)
        • střední hodnota bude odpovídat pravděpodobnosti, že konkrétní výška patří ženě
      • v M-kroku upravíme hodnoty $\mu_0,\mu_1$, abychom maximalizovali likelihood modelu
        • tedy spočítáme vážený průměr výšek
        • váhy odpovídají pravděpodobnosti, že výška patří muži (u $\mu_0$) / ženě (u $\mu_1$)
      • poznámka: může se jednoduše stát, že nám parametry $\mu_0,\mu_1$ vyjdou naopak (EM je metoda učení bez učitele, hledá vzory v datech, nezajišťuje jejich intepretaci)
• pasivní zpětnovazební učení (definice, metody ADP a TD)
  • uvažujeme agenta, který se účastní MDP (markovského rozhodovacího procesu)
  • pasivní učení – známe strategii $\pi$ (je pevně daná) a učíme se, jak je dobrá (učíme se utility funkci)
  • agent nezná přechodový model ani reward function
  • přímý odhad utility
    • máme trace (běh) mezi stavy, z toho počítáme utility function
    • odhadujeme užitky jednotlivých stavů
      • užitek stavu = reward-to-go (tedy odměna tohoto a všech budoucích stavů)
      • odměny z budoucích stavů bychom mohli zohleďnovat s discount factorem $\gamma$ (viz výše)
    • užitky pro jednotlivé stavy prostě průměrujeme
    • v podstatě učení s učitelem – na vstupu je stav, na výstupu užitek stavu (neboli reward-to-go)
    • nevýhoda
      • utilities nejsou nezávislé, ale řídí se Bellmanovými rovnicemi
      • hledáme v prostoru hypotéz, který je výrazně větší, než by musel být (obsahuje spoustu funkcí, co porušují Bellmanovy rovnice) → algoritmus konverguje pomalu
  • adaptivní dynamické programování (ADP)
    • agent se učí přechodový model a odměny
    • přechodový model odhaduje přímo z pozorovaných přechodů
    • utilitu počítá z Bellmanových rovnic třeba pomocí value iteration
      • využíváme toho, že užitky nejsou nezávislé
    • ADP zajišťuje, že jsou odhady užitků konzistentní
  • temporal-difference (TD) learning
    • upravuje stav, aby odpovídal aktuálně pozorovanému následníkovi
    • když dojde k přechodu ze stavu $s$ do stavu $s'$, tak na $U^\pi(s)$ použijeme update: $U^\pi(s)\leftarrow U^\pi(s)+\alpha\cdot (R(s)+\gamma\cdot U^\pi(s')-U^\pi(s))$
      • $\alpha$ je learning rate
    • vlastnosti
      • nepotřebuju přechodový model (je to model-free metoda)
      • konverguje to pomaleji než ADP
• aktivní zpětnovazební učení (definice, explorace vs. exploitace, Q-učení, SARSA)
  • uvažujeme agenta, který se účastní MDP (markovského rozhodovacího procesu)
  • aktivní učení – agent se učí strategii (policy; jak se rozhodovat) a taky utility funkci
  • mohli bychom použít ADP, tím vznikne hladový agent, který opakuje zažité vzory (nezkouší nové věci)
  • jak může volba optimální akce vést k suboptimálním výsledkům?
    • naučený model není stejný jako reálné prostředí
    • akce nejsou pouze zdrojem odměn, ale také přispívají k učení – ovlivňují vstupy
    • zlepšováním modelu se postupně zvětšují odměny, které agent získává
  • je potřeba najít optimum mezi exploration a exploitation
    • pure exploration – agent nepoužívá naučené znalosti
    • pure exploitation – riskujeme, že bude agent pořád dokola opakovat zažité vzory
    • základní myšlenka: na začátku preferujeme exploration, později lépe rozumíme světu, takže nepotřebujeme tolik prozkoumávat
  • exploration policies
    • první možná exploration policy: agent si zvolí náhodnou akci s pravděpodobností $\frac1t$ (kde $t$ je čas), jinak se řídí hladovou strategií
      • nakonec to konverguje k optimální strategii, ale může to být extrémně pomalé
    • rozumnější přístup je přiřadit váhu akcím, které agent ještě nevyzkoušel
    • existuje alternativní TD metoda, říká se jí Q-learning
      • $Q(s,a)$ označuje hodnotu toho, že provedeme akci $a$ ve stavu $s$
      • q-hodnoty jsou s utilitou ve vztahu $U(s)=\max_a Q(s,a)$
      • můžeme napsat omezující podmínku $Q(s,a)=R(s)+\gamma\sum_{s'} P(s'\mid s,a)\cdot \max_{a'}Q(s',a')$
        • tohle vyžaduje, aby se model naučil i $P(s'\mid s,a)$
      • Q-learning ale nevyžaduje model přechodů – je to bezmodelová (model-free) metoda, potřebuje akorát q-hodnoty
      • $Q(s,a)\leftarrow Q(s,a)+\alpha\cdot (R(s)+\gamma\cdot\max_{a'}Q(s',a')-Q(s,a))$
        • počítá se, když je akce $a$ vykonána ve stavu $s$ a vede do stavu $s'$
    • state-action-reward-state-action (SARSA)
      • je to varianta Q-learningu
      • $Q(s,a)\leftarrow Q(s,a)+\alpha\cdot (R(s)+\gamma\cdot Q(s',a')-Q(s,a))$
        • pravidlo se aplikuje na konci pětice $s,a,r,s',a'$, tedy po aplikaci akce $a'$
    • pro hladového agenta (který volí podle největšího $Q$) jsou algoritmy SARSA a základní Q-learning stejné
      • rozdíl je vidět až u agenta, který není úplně hladový, ale provádí i průzkum (exploration)
    • u SARSA se bere v úvahu reálně zvolená akce
      • SARSA je on-policy – jeho strategie se upravuje přímo za běhu algoritmu
      • Q-learning je off-policy – algoritmus se učí optimální strategii, ale během učení se může používat úplně jiná strategie
  • při aktivním učení je výhodnější učit se q-hodnoty než užitkovou funkci
    • abychom našli nejvýhodnější akci v daném stavu pomocí utility, museli bychom při výpočtu použít pravděpodobnost, že danou akcí přejdeme do určitého stavu
    • q-hodnota nám dá přímo řekne, jak je užitečné provést danou akci – k volbě nejlepší akce nepotřebujeme přechodový model