matice
- reálná matice typu m × n je obdélníkové schéma (tabulka) reálných čísel (v kulatých závorkách)
- prvek na pozici matice A (i-tý řádek, j-tý sloupec) značíme nebo
- ...
vektor
- sloupcový vektor – matice typu n × 1
- řádkový vektor – matice typu 1 × n
- standardně uvažujeme vektory sloupcové
- množina n-rozměrných vektorů se značí
- obecné matice značíme velkými písmeny, vektory malými písmeny
notace
- i-tý řádek matice A se značí
- j-tý sloupec matice A se značí
soustava lineárních rovnic
- mějme soustavu m lineárních rovnic o n neznámých ...
- matice soustavy je matice levé strany
- rozšířená matice soustavy obsahuje i pravou stranu (b)
geometrický význam soustavy rovnic
- nejprve případ m = n = 2, tedy dvě rovnice o dvou neznámých
- za obecných předpokladů ( nebo ) popisuje první rovnice přímku v rovině R^2 a analogicky druhá rovnice
- řešení soustavy leží v průsečíku dvou přímek
- tři rovnice o třech neznámých – průnik rovin může být i prázdná množina
- obecně rovnice určují tzv. nadroviny
elementární řádkové úpravy
- vynásobení i-tého řádku reálným číslem (tj. vynásobí se všechny prvky řádku)
- přičtení -násobku j-tého řádku k i-tému, přičemž a
- výměna i-tého a j-tého řádku
tvrzení: elementární řádkové operace zachovávají množinu řešení soustavy
- idea důkazu – základní myšlenkou je ukázat, že elementární úpravou se množina řešení nemění
výměna řádků pomocí ostatních úprav
- od j-tého řádku odečtu i-tý
- j-tý řádek přičtu k i-tému (na i-tém je nyní j-tý)
- od j-tého odečtu j-tý (na j-tém je nyní i-tý)
- j-tý řádek vynásobím
odstupňovaný tvar matice (REF)
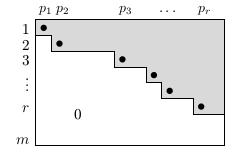
- řádky 1, ..., r jsou nenulové
- řádky r + 1, ..., m jsou nulové
- pod každým pivotem (tečka na obrázku) jsou samé nuly
- ...
- bázický a nebázický sloupec
hodnost matice
- počet nenulových řádků po převodu do odstupňovaného tvaru, značíme
algoritmus REF(A)
- buď
- if pro všechna a , then konec
- j := min{l; l>= j, akl not 0 pro nějaké k >= i} (přeskočíme nulové podsloupečky)
- urči , k>= i a vyměň řádky Ai* a Ak* (nyní je na pozici pivota hodnota )
- pro všechna k>i polož Ak* := Ak* - akj/aij Ai* (druhá elementární úprava)
- polož i := i + 1, j := j + 1 a jdi na krok 2
algoritmus (Gaussova eliminace)
- buď dána soustava rovnic (A | b), kde A náleží R^m×n, b náleží R^m
- převedeme rozšířenou matici soustavy (A | b) na odstupňovaný tvar (A' | b') a označíme r = rank (A | b)
- nyní nastala právě jediná z následujících tří situací
- soustava nemá řešení
- pokud poslední soupec je bázický, čili v posledním sloupci je pivot, tudíž rank(A) < rank(A | b)
- nula se rovná něčemu nenulovému
- soustava má alespoň jedno řešení
- soustava má jediné řešení – pokud r = n, pivoty jsou na diagonále, poslední sloupec je nebázický
- soustava má nekonečně mnoho řešení – pokud r < n, v matici je více nebázických sloupců
- bázické proměnné jsou ty, které odpovídají bázickým sloupcům
- nebázické proměnné jsou ty zbývající... parametry...
- soustava nemá řešení
řešitelnost soustavy a hodnost matice
- hodnost matice (A | b) udává řešitelnost a počet významných rovnic v soustavě
- Frobeniova věta:
Soustava (A | b) má alespoň jedno řešení právě tehdy, když .
důkaz komutativity
- A + B = B + A
- (A + B)ij = aij + bij
- (B + A)ij = bij + aij
- aij + bij = bij + aij, neboť aij, bij jsou reálná čísla, mezi nimiž platí při sčítání komutativita
i-tý jednotkový vektor
- na pozici i má jedničku, všude jinde nuly
- jednotková matice se skládá z jednotkových vektorů
matice a lineární zobrazení
numerická stabilita při řešení soustav – pozor na zaokrouhlení!
Hilbertova matice
řešení nestability – pomocí parciální pivotizace
interpolace polynomem