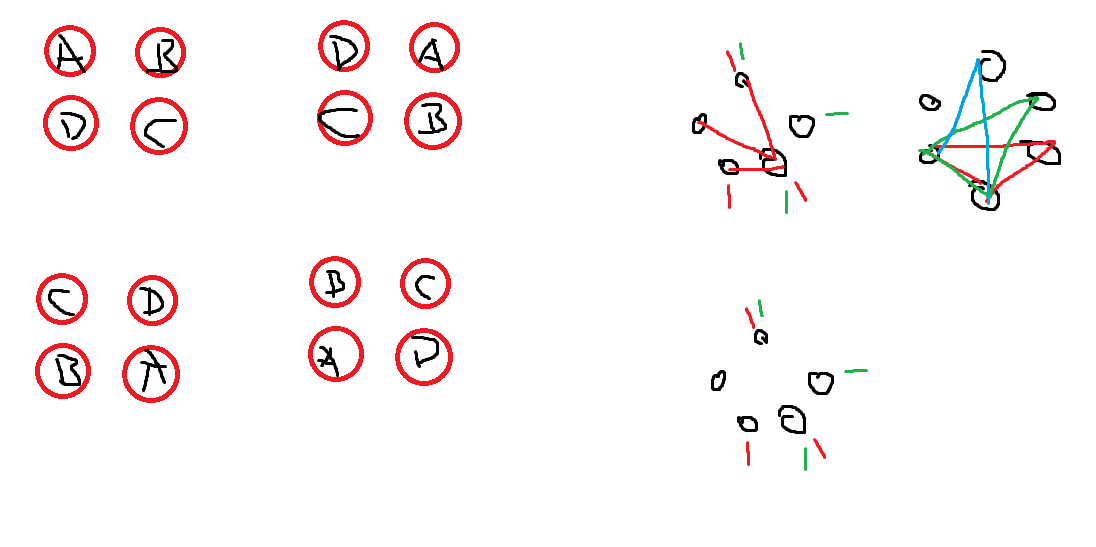
Algoritmizace: cvičení: kartičky | algoritmizace-programovani1

příklady z první hodiny

1b – hledáme nejtěžší minci (n – 1)
- proč to nejde rychleji?
- k vytvoření souvislého grafu o n vrcholech je potřeba n–1 hran (-> strom)
1c – hledáme druhou nejtěžší minci
- vážení po dvojicích, najdeme nejtěžší, mince, které jsme s ní porovnávali, si dáme stranou a hledáme nejtěžší mezi nimi
1d – robot se 3 rukama (2n – 3)
- proč to nejde rychleji?
- robot musí držet dosud 2 nejtěžší -> použije 2 ruce
- nevíme, která mince je správná, takže musíme vzít všechny
- kandidáta poměříme s 1. nebo 2.
- lze vynutit poměření kandidáta s oběma (v nejhorším případě)
1e – nejtěžší poštou
- vážení každého s každým → $\frac{n^2-n}{2}$
2 – průchod tunelu (12 minut)
- 2 otec s matkou
- 1 otec
- 5 syn s dcerou
- 2 matka
- 2 otec s matkou
3 – kelímkomat

kelímkomat

pozorování
- můžeme táhnout 1) vedle sebe, 2) úhlopříčně
- umíme sáhnout na 3 různé kelímky, kelímkomat nám může 1 kelímek skrýt
- chceme úhlopříčně kelímky
b) robot
- plní příkazy – otoč kelímek, otoč dnem vzhůru, otoč dnem dolů, nech tak
- nepoví nám stav
- kroky 1 a 2 jsou stejné – všechny dnem vzhůru kromě jednoho
- krok 3 – vedle sebe jeden otoč
- krok 4 – úhlopříčně oba otoč
- krok 5 – vedle sebe oba otoč
c) pět kelímků – neexistuje poslední krok
d) ukázat totéž
e) ?

vážení mince

logaritmus o základu dva – kolikrát musím rozpůlit hromádku věcí, aby mi zbyla jedna věc
dolní odhad – tu nejtěžší chci vážit s co nejméně mincemi

doma rozmyslet 3d, 3e, 1e (proč nemůže chybět jeden)

1e – chybějící informace o vztahu dvou mincí by mohla zapříčinit, že bychom věděli o dvou nejtěžších mincích, ale nevěděli bychom, která z nich je těžší
3d – neexistuje "souměrné" rozložení kelímků, při kterém by nezáviselo na otočení kelímkomatu, tedy neexistuje poslední krok
3e – poslední krok existuje, je to situace, kdy se stavy kelímků střídají (každý je otočený jinak než ty vedle něj)
- uděláme 3 kroky, které zajistí, že právě jeden kelímek je otočený špatně

Teorie

složitost problému třídní porovnáním

rozhodovací strom bude mít nějaký počet hladin, což bude výsledná složitost algoritmu
těchto hladin bude nejméně log n!, protože listů musí být nejméně n!
n! se dá odhadnout

Teorie

třídění haldou